רודולף שטיינר

GA324a

תרגום מרומנית: מ. ברכה

עריכת תרגום: דניאל זהבי

תיקונים: דליה דיימל

לספר ראו כאן

הרצאה מספר 8

אודות החלל הרב ממדי

22.10.1908   ברלין

בנושא של היום נתמודד עם מספר קשיים ויש להתייחס להרצאה זו שנערכת לבקשתכם כפרק בסדרת הרצאות. כדי להבין בהמשך את הנושא, אפילו ברמה הפורמלית, יש צורך בידע מתמטי כלשהו. אך הבנת הנושא על כל מציאותו דורשת חדירה עמוקה לאזוטריות. היום נוכל לטפל בנושא זה באופן שטחי מאוד, ולספק רק גירוי לחלקכם.

קשה מאוד לדבר על ממדים גבוהים יותר מכיוון שכדי ליצור דעה על משהו שהוא יותר משלושת הממדים הרגילים עלינו להיכנס לתחומים מופשטים, וכאן עלינו להבין את המושגים שלנו בצורה מדויקת וקפדנית, אחרת נגיע למשהו נטול בסיס. זה היה גורלם של אנשים רבים שאנו מכירים, חברים ואויבים כאחד.

הרעיון של חלל רב ממדי אינו זר למתמטיקאים כפי שנהוג לחשוב.^[1] מתמטיקאים כבר עושים חישובים הכוללים פעולות רב ממדיות. כמובן, מתמטיקאים יכולים לדבר רק על חלל רב ממדי במידה מצומצמת ביותר; בעצם, הם יכולים לדון רק באפשרות קיומם. יש לקבוע אם חלל כזה הוא אמיתי או לא, בידי מי שיכול להסתכל עליו. כאן אנו עוסקים רק במושגים טהורים, שאם יובנו במדויק, באמת יבהירו את מושג החלל שלנו.

מהו חלל? בדרך כלל אנו אומרים שהחלל נמצא סביבנו, שאנו עוברים בחלל וכן הלאה. מי שרוצה לקבל מושג ברור יותר של החלל חייב להיכנס להפשטות מסוימות. אנו קוראים לחלל בו אנו נעים תלת ממד. הוא משתרע כלפי מעלה וכלפי מטה, ימינה ושמאלה, קדימה ואחורה. כאשר אנו מסתכלים על עצמים אנו רואים אותם מתרחבים בחלל התלת ממדי, כלומר בעלי אורך, רוחב וגובה מסוימים.

אולם עלינו להתמודד עם פרטי מושג החלל, אם נרצה לרכוש מושג מדויק יותר. בואו נסתכל על הצורה המוצקה הפשוטה ביותר, הקובייה. היא מראה לנו בצורה הברורה ביותר מהו אורך, רוחב וגובה. האורך והרוחב של בסיס הקובייה שווים. כאשר אנו מרימים משטח זה עד שגובהו מעל המיקום ההתחלתי זהה לאורכו ולרוחבו, מתקבלת קובייה, כלומר צורה תלת ממדית. בעזרת הקובייה נוכל ליידע את עצמנו בצורה הברורה ביותר אודות פרטי המבנה התלת ממדי. כאשר אנו בוחנים את גבולות הקובייה אנו מגלים שהם מורכבים ממשטחים שטוחים המחוברים על ידי צדדים באורכים שווים. לקובייה יש שישה משטחים שטוחים כאלה.

מהו משטח שטוח? בשלב זה, אלה שאינם מסוגלים להפשטות קיצוניות יתחילו למעוד. למשל, אי אפשר להפריד על ידי חיתוך של אחת מהדפנות של קוביית שעווה, שכבה דקה מאוד של שעווה, כי תמיד נקבל שכבה בעובי מסוים – כלומר אובייקט מוצק. אנחנו לא יכולים להגיע לגבול הקובייה בדרך הזו. הגבול האמיתי שלה הוא רק אורך ורוחב, אך לא עובי. כך אנו מגיעים לנוסחה: משטח שטוח הוא הגבול של צורה תלת ממדית ויש לו ממד אחד פחות.

אם כן, מהו הגבול של משטח שטוח כגון ריבוע? שוב, ההגדרה דורשת את רמת ההפשטה הגבוהה ביותר. הגבול של צורה מישורית הוא קו בעל ממד אחד בלבד, אורך. הרוחב הוסר. מהו הגבול של קטע ישר? זו נקודה שאין לה ממד. כך אנו תמיד מבטלים ממד אחד כדי למצוא את הגבול של צורה גיאומטרית.

הבה נעקוב אחר קו המחשבה של מתמטיקאים רבים, כולל ריימן, שעשה עבודה יוצאת דופן בתחום זה. נחשוב על נקודה, שאין לה ממד; קו, שיש לו ממד אחד; מישור, שיש בו שני ממדים; וחפץ מוצק, שיש לו שלושה ממדים. ברמה הטכנית גרידא מתמטיקאים תוהים אם אפשר להוסיף עוד ממד רביעי. אם כן, הגבול של צורה בעלת ארבעה ממדים צריך להיות צורה תלת ממדית, כפי שמישור הוא הגבול של גוף מוצק, קו הגבול של מישור הוא קו ונקודה היא הגבול של קו. כמובן, מתמטיקאים יכולים לחשוב על צורות עם חמישה ממדים, שישה, שבעה ואפילו X ממדים, כאשר X הוא מספר שלם חיובי.

בנקודה זו יש עמימות מסוימת כאשר אנו אומרים שלנקודה אין ממדים, לקו יש ממד אחד, למישור שני ממדים ולאובייקט מוצק שלושה ממדים. אנו יכולים ליצור חפצים מוצקים, כגון קוביות, מכל חומר – שעווה, כסף, זהב וכן הלאה. החומרים שונים, אך אם נבנה אותן באותו גודל, כל אחת תתפוס את אותו נפח בחלל. אם לאחר מכן נסלק את כל החומרים האלה שהקוביות מכילות, נותר לנו רק מקטעי שטח ספציפיים מסוימים, התמונות המרחביות של הקובייה. מקטעי החלל הללו זהים בכל הקוביות, ללא קשר לחומר ממנו הן עשויות, ולכולם יש אורך, רוחב וגובה. אנו יכולים לדמיין מרחבים קובייתיים כאלה המשתרעים עד אינסוף, ובכך גורמים לחלל תלת ממדי אינסופי. האובייקט החומרי הוא רק קטע של חלל זה.

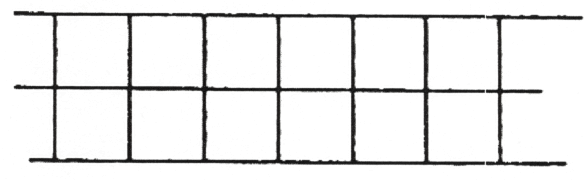
השאלה הבאה היא האם נוכל להרחיב הערכות מושגיות כאלה, שתחילתן בחלל, למציאות גבוהה יותר? למעשה, עבור המתמטיקאי חשיבה שכזו כוללת רק חישובים שכרוכים במספרים בלבד. האם זה מותר? כפי שאראה לכם, שימוש במספרים לחישוב גודלם של החללים יכול להיות מבלבל מאוד. למה? מספיק להגיד לכם דבר אחד. תארו לעצמכם שיש לכם צורה מרובעת. אני יכול להרחיב צורה שטוחה זו לשני הכיוונים, עד שנגיע לצורה שטוחה המשתרעת עד אינסוף בין שני קווים (איור 56).

איור 56

מכיוון שצורה מישורית זו מורחבת עד אינסוף, גודלה אינסופי (∞). עכשיו נניח שאנשים אחרים שומעים שהשטח בין שני הקווים האלה הוא אינסופי. באופן טבעי, אנשים אלה חושבים על אינסוף. אבל אם אתה מדבר איתם על אינסוף, הם עשויים, בתנאים מסוימים, לקבל מושגים שגויים לחלוטין לגבי מה שאתה רוצה להגיד. נניח שאני מוסיף ריבוע לכל אחד מאלו הקיימים, כלומר שורה שנייה של ריבועים רבים אינסופיים. התוצאה היא שוב אינסוף, אבל אינסוף אחר שגדול פי שניים מהראשון (איור 57). לכן, ∞ = 2∞.

באותו אופן אני יכול להגיע ל ∞ = 3∞. בחישובים מספריים ניתן להשתמש באינסוף בקלות כמו כל מספר סופי אחר. כשם שזה נכון שבמקרה הראשון החלל הוא אינסופי, נכון באותה מידה כי מאוחר יותר הוא 2∞, 3∞ וכן הלאה. זה מה שמתרחש כאשר אנחנו מחשבים במספרים.

איור 57

אתם רואים כיצד מושג החלל האינסופי הקשור לגישה מספרית אינו נותן לנו שום אפשרות לחדור עמוק יותר למציאות גבוהה יותר. למספרים אין שום קשר לחלל, ממש כמו אפונה או כל חפץ אחר. החישובים לא משנים כלל את המציאות. אם יש לנו שלושה אפונים, הכפלה לא יכולה לשנות עובדה זו גם אם נכפיל נכון. בחישוב 3 כפול 3 = 9 לא נקבל תשעה אפונים. חשיבה פשוטה לא משנה דבר במקרים כאלה, וחישובים מספריים הם חשיבה פשוטה. נשארתי עם שלושה אפונים, לא תשעה, למרות שעשיתי את פעולת הכפל באופן נכון. באורח דומה, למרות שהמתמטיקאים מבצעים חישובים כאלה בנוגע לשניים, שלושה, ארבעה או חמישה ממדים, החלל שאנו מתמודדים איתו הוא תלת ממדי בלבד. אני בטוח שאולי תתפתו מחישובים מתמטיים שכאלה, אך הם רק מוכיחים שאפשר לבצע חישובים על חלל רב ממדי. המתמטיקה לא באמת יכולה להוכיח שחלל רב ממדי באמת קיים; היא אינה יכולה להוכיח כי מושג זה תקף במציאות. אנחנו צריכים להיות מאוד ברורים בנקודה זו.

נתמקד כעת בשיקולים אחרים שהביאו המתמטיקאים בשנינות רבה. אנו בני האדם חושבים, שומעים וחשים בחלל התלת ממדי. הבה נדמיין ישויות המסוגלות לתפוס רק בחלל דו ממדי. ישויות כאלה אפשר להעלות על הדעת לחלוטין. ארגון הגוף שלהם יאלץ אותם להישאר במישור, כך שהן לא תוכלנה לעזוב את הממד השני. הן תוכלנה לנוע ולתפוס רק ימינה ושמאלה, קדימה ואחורה. לא יהיה להן מושג לגבי שום דבר שקיים מעליהן או מתחתיהן.^[2]

המצב שלנו במרחב התלת ממדי יכול להיות דומה. הארגון הגופני שלנו יכול להיות מותאם כל כך לחלל התלת ממדי, עד שאיננו יכולים לתפוס את הממד הרביעי, אלא רק להסיק אותו, כשם שיצורים דו ממדיים צריכים להסיק את קיומו של הממד השלישי. מתמטיקאים אומרים שאכן אפשר לחשוב על האדם כמוגבל בצורה מסוימת זו. כמובן שאפשר גם לומר שזו גם יכולה להיות פרשנות שגויה. כאן נדרשת שוב גישה הרבה יותר מדויקת, אם כי הנושא אינו פשוט כמו הדוגמה הראשונה בה ניסינו להשתמש במספרים כדי להבין את אינסופיותו של החלל. היום אגביל את עצמי בכוונה להסברים פשוטים.

המצב הנוגע למסקנה זו אינו זהה למצב של קו המחשבה הראשון, של חישוב מתמטי לחלוטין. במקרה זה, אנו באמת מגיעים לנקודה שבה יש מה לאחוז. נכון שיכולה להיות ישות שיכולה לתפוס רק את מה שנע במישור. ישות כזו לא תהיה מודעת לחלוטין לכך שיש משהו מעליה או מתחתיה. תארו לעצמכם שנקודה במישור הופכת גלויה לאותה ישות. כמובן, הנקודה גלויה רק ​​מכיוון שהיא נמצאת באותו מישור. כל עוד הנקודה נעה במישור היא נשארת גלויה, אך ברגע שהיא זזה מהמישור היא הופכת לבלתי נראית. מנקודת המבט של הישות הדו ממדית היא נעלמה. ועכשיו נניח שהנקודה מופיעה מחדש במקום אחר, הופכת שוב לגלויה, שוב נעלמת וכן הלאה. כאשר הנקודה יוצאת מהמישור, הישות הדו ממדית אינה יכולה לעקוב אחריה, אך היא יכולה לומר לעצמה: "בינתיים הנקודה נמצאת במקום שאני לא יכולה לראות אותה". ישות המישור יכולה לעשות שני דברים. בואו נתגנב לנפשה של הישות הדו ממדית הזו. היא יכולה לומר, "יש ממד שלישי שבו אובייקט נעלם ואז מופיע שוב." או שהיא יכולה גם לומר, "רק טיפשים יכולים לדבר על הממד השלישי. החפץ פשוט נעלם ובכל פעם שהוא מופיע הוא נוצר מחדש". במקרה האחרון עלינו לומר שהישות הדו ממדית חוטאת נגד ההיגיון. אם היא לא רוצה להניח שהאובייקט מתפורר ומשוחזר שוב ושוב, אז עליה להכיר בכך שהאובייקט נעלם איפשהו במקום שאינה יכולה לראותו.

כאשר כוכב שביט נעלם, הוא עובר דרך חלל בעל ארבעה ממדים.^[3]

כעת אנו רואים מה צריך להוסיף לגישה המתמטית בנושא זה. צריך למצוא משהו בתחום ההתבוננות שלנו שמופיע ונעלם שוב ושוב. לשם כך אין צורך ביכולות על-חושיות. אם הישות הדו ממדית הייתה יכולה לראות באופן על-חושי, היא הייתה יודעת מניסיון שיש ממד שלישי ולא היה עליה להסיק את קיומו. אותו דבר לגבי האדם. כל עוד אין לו יכולת ראיה על-חושית, הוא נאלץ לומר: "אני מוגבל לשלושה ממדים, אך ברגע שאני מבחין במשהו שנעלם ומופיע מעת לעת, אני רשאי לומר שמדובר בממד רביעי".

על כל מה שנאמר עד כה אין עוררין והאישור כה פשוט עד שהאדם, במצב העיוורון הנוכחי שלו, אפילו לא יחשוב לקבל אותו. התשובה לשאלה: האם יש משהו שנעלם ומופיע שוב ושוב? היא מאוד קלה. חישבו רק על השמחה שלפעמים מתעוררת בכם ואז נעלמת. מישהו שאינו בעל יכולת ראיה על-חושית לא יוכל לקלוט אותה שוב. ואז אותה תחושה מופיעה מחדש עקב אירוע כלשהו. כעת, כמו הישות הדו ממדית, אתם יכולים להתנהג בשתי דרכים. או שתגידו לעצמכם שהתחושה נעלמה בחלל שבו אינכם יכולים לעקוב אחריה, או שתחשבו שהתחושה נעלמה ונוצרת שוב מחדש בכל פעם שהיא מופיעה.

האמת היא שכל מחשבה שנעלמת אל הלא מודע היא הוכחה שמשהו נעלם ואז מופיע שוב. לכל היותר ניתן להתנגד לדברים הבאים. אם מושג זה נראה לכם סביר, הצעד הבא הוא לנסח את כל ההתנגדויות האפשריות שיכולות להתעורר על ידי תפיסה חומרית. כעת אזכיר את ההתנגדות הרלוונטית ביותר; בכל האחרים קל מאוד להילחם. אנשים עשויים לטעון שהכל מוסבר בצורה חומרית בלבד. אני רוצה לתת לכם דוגמה לכך שמשהו יכול להיעלם ולהופיע מחדש בתהליכים חומריים. תארו לעצמכם בוכנת אדים בפעולה. כל עוד הכוח פועל על הבוכנה אנו קולטים את תנועתה. כעת נניח שאנו מפצים על תנועתה בעזרת בוכנה זהה, הפועלת בכיוון ההפוך. התנועה נעצרת והמכונות נשארות ללא תנועה. התנועה נעלמת.

באופן דומה, אנשים עשויים לטעון כי תחושת ההנאה אינה אלא תנועה של מולקולות במוח. כל עוד המולקולות נעות, אני חווה הנאה. נניח שגורם אחר גורם לתנועה הפוכה של מולקולות. ההנאה נעלמת. מישהו שלא עוקב עמוק מספיק אחר קו מחשבה זה, עשוי לגלות שאכן מדובר בטיעון חשוב כנגד הרעיונות שהוצגו קודם לכן. אך בואו נסתכל מקרוב על ההתנגדות הזו. בדיוק כפי שתנועת הבוכנה נעלמה כתוצאה מתנועה הפוכה, כך גם אומרים כי תחושה שמבוססת על התנועה המולקולרית מתבטלת על ידי תנועה מולקולרית הפוכה. מה קורה כאשר תנועת בוכנה אחת מפוצה על ידי תנועתה של השנייה? שתי התנועות נעלמות. התנועה השנייה לא יכולה לחסל את הראשונה מבלי לחסל את עצמה. התוצאה היא היעדר תנועה מוחלט; לא נשארת תנועה. באופן דומה אף תחושה הקיימת בתודעתי לא תוכל לחסל תחושה אחרת מבלי לחסל את עצמה במקביל. לפיכך, ההנחה שתחושה אחת יכולה לחסל אחרת היא שקרית לחלוטין. אחרת לא תישאר תחושה והעדר מוחלט של תחושה ייגרם. אפשר לומר לכל היותר שהתחושה הראשונה יכולה להידחק על ידי השנייה אל התת מודע. אך כשאנו אומרים זאת אז אנו מודים שיש משהו שחמק מההתבוננות הישירה שלנו.

היום דיברנו רק על רעיונות מתמטיים גרידא מבלי לשקול כלל תפיסה שמעבר לחושים. כעת, לאחר שהכרנו באפשרות של קיום עולם בעל ארבעה ממדים שכזה, אנו יכולים לשאול את עצמנו האם אנו יכולים להתבונן באובייקט בעל ארבעה ממדים מבלי להיות בעלי ראיה על-חושית. הטלה מסוג מסוים מאפשרת לנו לעשות זאת. אנו יכולים לסובב צורה שטוחה עד שהצל שהיא מטילה הופך לקו. באופן דומה, צל של קו יכול להיות נקודה ותמונת הצל של אובייקט תלת ממדי היא צורה מישורית דו ממדית. לפיכך, ברגע שנשתכנע בקיומו של ממד רביעי, טבעי לומר כי צורות תלת ממדיות הן תמונות צל של צורות בעלות ארבעה ממדים.

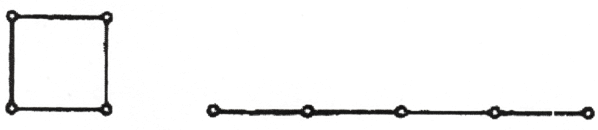איור 58

זוהי דרך גיאומטרית אחת לדמיין חלל בעל ארבעה ממדים. אך יש גם דרך אחרת לראות זאת עם גיאומטריה. תארו לעצמכם ריבוע בעל שני ממדים. עכשיו דמיינו את ארבעת הקטעים התוחמים אותו מתיישרים ויוצרים קו יחיד. פרשתם את צורות הגבול של צורה דו ממדית באופן שהן ממוקמות בממד אחד (איור 58). בואו ונמשיך. תארו לעצמכם קטע של קו. אנו ממשיכים באותו אופן כפי שעשינו עם הריבוע (הסרת ממד אחד), כך שהגבולות של הצורה מצטמצמות לשתי נקודות. לפיכך, תיארנו את גבולות הצורה החד ממדית באפס ממדים. אנו יכולים גם לפרוש קובייה על ידי השטחתה לשישה ריבועים (איור 59). אנו פורשים את גבולות הקובייה כך שהם מונחים במישור. בדרך זו אנו יכולים לומר שניתן לתאר קו כשתי נקודות, ריבוע כארבעה מקטעי קו וקובייה כשישה ריבועים. שימו לב לרצף המספרים: שניים, ארבעה, שישה.

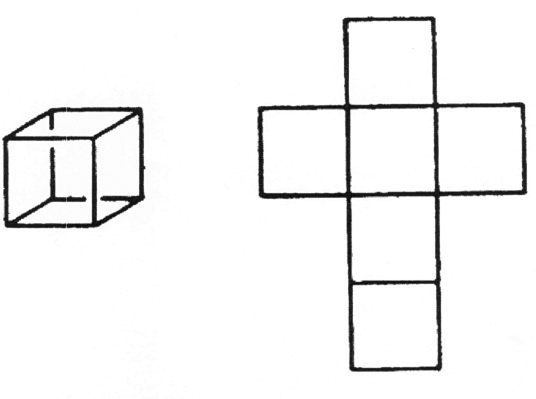איור 59

לאחר מכן ניקח שמונה קוביות. כפי שהדוגמאות הקודמות היו מורכבות מהגבולות הפרושים של צורות גיאומטריות, כך שמונה הקוביות יוצרות את גבולותיה של צורה בעלת ארבעה ממדים (איור 60). פרישת הגבולות הללו מראה צלב כפול, המייצג את הגבולות של צורה בעלת ארבעה ממדים. הינטון מכנה את קוביית הארבעה ממדים – טסרקט.

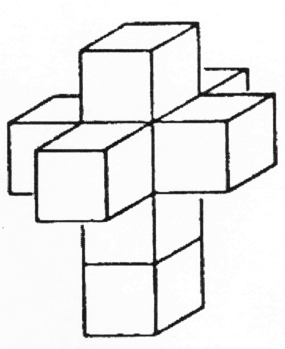איור 60

תרגיל זה נותן לנו רעיון של גבולות הטסרקט. הרעיון שלנו לגבי צורה בעלת ארבעה ממדים זהה לרעיון של קובייה שיכולה להיות לישויות דו ממדיות על ידי פרישת גבולות קובייה.

———————————————————————————

1. המחקרים המתמטיים הראשונים בנושא בעיית המרחב הרב ממדי מתוארכים מאמצע המאה ה-19. ↑
2. ראו גם את הספרים הבאים, שהיו ידועים ופופולריים בימיהם: Abbott, העולם השטוח [1884], הינטון, הפרק "עולם שטוח", ברומנים מדעיים [1886] (עמ '129-159). ↑
3. ראו גם הרצאתו של רודולף שטיינר מיום 10 באפריל 1912 (GA136) יצא לאור בעברית בהוצאה פרטית בשם: ישויות רוחיות בגופים השמימיים ובממלכות הטבע. לא הצלחנו לאשר את ההנחה שהצהרה זו של שטיינר מתייחסת לתפיסתו של צולנר בנושא זה. תורת השביטים של צולנר (ראו צולנר [1886]) הפכה לבסיס ונקודת המוצא לתורת השביט הקונבנציונלית המודרנית, ואין כל אינדיקציה לכך שצולנר ראה קשר בין תורת השביטים שלו לבין רעיונות רוחניים על חלל בעל ארבעה ממדים. ↑