הממד הרביעי
רודולף שטיינר
GA324a
תרגום מרומנית: מ. ברכה
עריכת תרגום: דניאל זהבי
תיקונים: דליה דיימל
לספר ראו כאן
הרצאה מספר 6
7.6.1905 ברלין
היום עלינו לסיים סדרת הרצאות זו על הממד הרביעי של החלל, למרות שבאמת הייתי רוצה להציג בפירוט רב יותר את המערכת המסובכת, אך אצטרך להציג הרבה מהדגמים האחרים של הינטון. כל מה שאני יכול לעשות זה להפנותכם לשלושת ספריו המעמיקים והברורים.[1] כמובן שמי שאינו רוצה להשתמש באנלוגיות כמו אלה שהוצגו בהרצאות הקודמות לא יוכל לקבל תמונה מנטלית של חלל בעל ארבעה ממדים. זה דורש דרך חדשה לפיתוח החשיבה.
עכשיו הייתי רוצה לפתח תמונה אמיתית (הטלה מקבילה) של טסרקט. ראינו שבחלל דו ממדי לריבוע יש ארבעה צדדים. המקבילה שלו בחלל התלת-ממדי היא הקובייה, בעלת שישה צדדים מרובעים (איור 42).
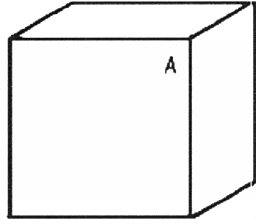 איור 42
איור 42
המקביל בעל הארבעה ממדים הוא הטסרקט, אשר תחוּם בשמונה קוביות. כתוצאה מכך, ההטלה של טסרקט לתוך חלל תלת-ממדי מורכבת משמונה קוביות שלובות זו בזו. ראינו כיצד שמונה הקוביות הללו יכולות לחפוף בחלל תלת ממדי. כעת אבנה הטלה אחרת של טסרקט.
תארו לעצמכם קובייה המוחזקת בצורה כזו שהאור משאיר צל על הלוח. כך שנוכל לצייר את הצל בעזרת גיר על הלוח (איור 43). כפי שניתן לראות, התוצאה היא משושה. אם תדמיינו את הקובייה שקופה תוכלו לראות שבהטלה שלה אל המישור, שלוש הפנים הקדמיות חופפות לשלוש הפנים האחוריות על אותו משטח, ויוצרות משושה.
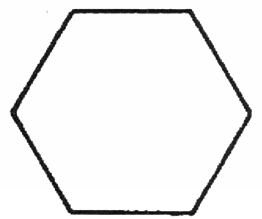 איור 43
איור 43
כדי לקבל הטלה שניתן ליישמה עבור טסרקט, אנא דמיינו את הקובייה שלפניכם ממוקמת בצורה כזו שהנקודה הקדמית A מכסה את הנקודה האחורית C. אם לאחר מכן תתעלמו מהממד השלישי, התוצאה היא שוב צל של משושה. תנו לי לצייר לכם זאת (איור 44).
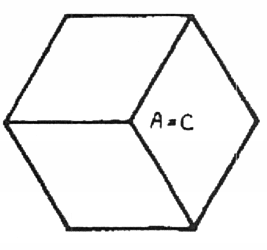 איור 44
איור 44
כשחושבים על הקובייה במצב הזה רואים רק את שלוש הפנים הקדמיות האלה; שלוש הפנים האחרות מוסתרות מאחור. כתוצאה מכך, פני הקובייה נראים מקוצרים וזוויותיה אינן עוד זוויות ישרות. מנקודת מבט זו, הקובייה נראית כמו משושה רגיל. כך יצרנו דימוי של הקובייה התלת ממדית במרחב הדו ממדי. מכיוון שהטלה זו מקצרת את דפנות הקובייה ומשנה את הזוויות, עלינו לדמיין את שש הפנים המרובעות של הקובייה כריבועים מעוותים, כמעוינים.
עכשיו נחזור על פעולת ההטלה שעשינו עם קובייה תלת ממדית במישור עם צורה בעלת ארבעה ממדים שאותה נטיל לחלל תלת ממדי. לשם כך נשתמש בהטלה מקבילה כדי לצייר טסרקט, צורה המורכבת משמונה קוביות בממד השלישי. בביצוע פעולה זו השגנו בקובייה שלושה צדדים גלויים ושלושה בלתי נראים, שכולם קיימים בחלל ואינם ממוקמים בפועל במישור ההטלה. עכשיו דמיינו קובייה מעוותת בצורה כזו שמתקבלת ממנה מקבילה מעוינת. אם תיקחו שמונה צורות כאלה תוכלו להרכיב את שמונה קוביות הטסרקט כך שהן חודרות אחת לשנייה ונפגשות פעמיים עם הקוביות המעוינות בדודקהדרון המעוין (איור 45).
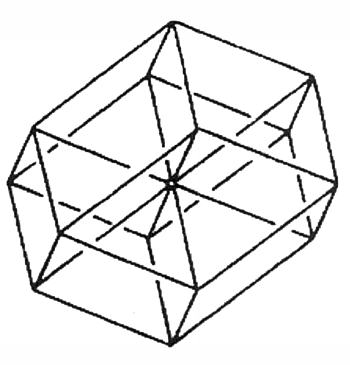 איור 45
איור 45
לצורה זו יש ציר נוסף מאשר לקובייה התלת ממדית. ברור שלצורה בעלת ארבעה ממדים יש ארבעה צירים. גם כשחלקיה משתלבים זה בזה, נותרים ארבעה צירים. לפיכך, הטלה זו מכילה שמונה קוביות החודרות אחת לשנייה, המוצגות כקוביות מעוינות. דודקהדרון מעוין הוא תמונה סימטרית, או תמונת צל, של טסרקט המוקרן לחלל תלת ממדי (איור 45).
הגענו ליחסים אלה באנלוגיה, אך היא תקפה לחלוטין. בדיוק כפי שהשגנו הטלה של קובייה במישור, כך ניתן לשרטט טסרקט על ידי הטלתו לחלל תלת ממדי. ההטלה המתקבלת מתנהגת כלפי הטסרקט כתמונת הצל של הקובייה ביחס לקובייה. אני חושב שפעולה זו קלה להבנה.
ברצוני לקשר בין מה שעשיתי זה עתה לתמונה הנפלאה שהציעו אפלטון ושופנהאואר במשל על המערה.[2]
אפלטון מבקש מאיתנו לדמיין אנשים כבולים במערה, כך שהם לא יכולים לסובב את הראש, ורואים רק את הקיר האחורי. מאחוריהם נושאים אנשים אחרים חפצים שונים דרך פתח המערה. אנשים וחפצים אלה הם תלת ממדיים, אך האסירים רואים רק את הצללים המוטלים על הקיר האחורי. הכל בחדר הזה יופיע רק כצללים דו ממדיים על הקיר הנגדי.
אפלטון אומר לנו שמצבנו בעולם דומה. אנחנו האנשים הכבולים במערה. למרות שאנו בעצמנו בעלי ארבעה-ממדים, כמו כל דבר אחר, כל מה שאנו יכולים לראות מופיע רק כתמונות בחלל תלת-ממדי.[3] לדברי אפלטון, אנו מצומצמים לראות רק את הצללים התלת ממדיים של הדברים, במקום את המציאות שלהם. אני רואה את היד שלי רק כתמונת צל; במציאות היא בעלת ארבעה ממדים. כל מה שאנו רואים הוא רק תמונת צל של המציאות בעלת הארבעה ממדים. כמו הטסרקט שהראיתי לכם.
כך, ביוון העתיקה, ניסה אפלטון להמחיש שהגופים המוכרים לנו הם למעשה בעלי ארבעה-ממדים וכי אנו רואים רק את תמונות הצל שלהם במרחב התלת ממדי. אמירה זו אינה שרירותית לחלוטין, כפי שאטען בקצרה. בהתחלה, אנו יכולים לומר, כמובן, כי מדובר בספקולציות בלבד. כיצד נוכל לדמיין שיש מציאות כלשהי בצורות אלה המופיעות על הקיר? אך תארו לעצמכם עכשיו שאתם יושבים כאן בשורה ולא יכולים לזוז. לפתע הצללים מתחילים לנוע. לא ניתן לדמיין שהצללים על הקיר יכולים לזוז מבלי לעזוב את הממד השני. כאשר תמונה נעה על הקיר היא מראה שמשהו מחוץ לקיר היה צריך לגרום לתנועה לחפץ האמיתי שאינו על הקיר. בחלל תלת ממדי אובייקטים יכולים לחלוף זה על פני זה, דבר שתמונות הצל שלהם לא יכולות לעשות, אם תדמיינו אותם בלתי חדירות – כלומר מורכבים מחומר. אם נדמיין לעצמנו שתמונות אלה עשויות מחומר, אזי הן לא יכולות לחלוף אחת על פני השנייה מבלי לעזוב את הממד השני.
כל עוד התמונות על הקיר נשארות דוממות, אין לי סיבה להסיק שמשהו קורה מחוץ לקיר, מחוץ לתחום של תמונות הצל הדו-ממדיות. ברגע שהן מתחילות לזוז, אני נאלץ לחפש את מקור התנועה ולהסיק כי מקורו של השינוי הוא מחוץ לקיר, בממד השלישי. כך השינוי בתמונות-הצל מבשר לנו שיש, מלבד הממד השני, ממד שלישי.
למרות שלתמונה יש מציאות מסוימת ותכונות ספציפיות, היא בכל זאת שונה במהותה מהאובייקט האמיתי. תמונת מראה היא גם ללא ספק תמונה בלבד. אתה רואה את עצמך במראה, אך אתה נוכח כאן בעת ובעונה אחת. ללא נוכחות של יסוד שלישי – כלומר ישות בתנועה – אינך יכול באמת לדעת מי מהם הוא אתה. תמונת המראה עושה אותן תנועות כמו המקור; אין לה את היכולת להזיז את עצמה, אלא היא תלויה באובייקט האמיתי, בישות. בדרך זו אנו יכולים להבחין בין התמונה לישות, ולומר שרק ישות יכולה לייצר שינוי או תנועה מתוך עצמה. אני מבין שתמונות הצל על הקיר אינן יכולות להזיז את עצמן; לכן הן אינן יכולות להיות ישויות. אני צריך ללכת מעבר לתמונות כדי לגלות ישויות.
עכשיו בואו ניישם את סדרת המחשבות הזו על העולם בכללותו. העולם הוא תלת ממדי, אך אם תתייחסו אליו כשלעצמו על ידי חיבוקו במחשבותיכם, תגלו שהוא למעשה בלתי נייד. גם אם תדמיינו שהוא קפוא בשלב כלשהו, הוא עדיין תלת ממדי. במציאות, העולם אינו אותו דבר בשני זמנים שונים. הוא משתנה. כעת דמיינו שהרגעים השונים האלה ייעלמו, אז מה שקיים, נשאר. אם לא היה זמן, העולם לעולם לא היה משתנה, אך גם ללא זמן או שינוי הוא עדיין יהיה תלת ממדי. באופן דומה, התמונות על הקיר נשארות דו ממדיות, אך העובדה שהן משתנות מרמזת על קיומו של ממד שלישי. עלינו לחפש בממד הרביעי את הסיבה לכך שהעולם משתנה כל הזמן, ובכל זאת נשאר תלת ממדי גם כשאין שינוי. יש לחפש את הסיבה לשינוי, את הגורם לשינוי מחוץ לממד השלישי. בשלב זה מבינים את קיומו של הממד הרביעי ואת ההצדקה למטפורה של אפלטון. כך אנו תופסים את כל העולם התלת ממדי כהטלת צל של עולם בעל ארבעה ממדים. השאלה היחידה היא כיצד עלינו להבין את המציאות של ממד רביעי זה.
כמובן שעלינו להבין שאי אפשר שהממד הרביעי ייכנס ישירות אל השלישי. הוא לא יכול לעשות זאת. הממד הרביעי לא יכול פשוט ליפול לתוך השלישי. כעת ברצוני להראות לכם כיצד לקבל את הרעיון של חציית הממד השלישי. באחת ההרצאות הקודמות שלי ניסיתי להעיר בכם רעיון דומה.[4] תארו לעצמכם שיש לנו עיגול שהולך וגדל, כך שכל קטע של העיגול נהיה יותר ויותר שטוח, בסופו של דבר הקוטר הופך להיות כה גדול עד שהעיגול הופך לקו ישר. לקו ישר יש רק ממד אחד, אך לעיגול יש שניים. כיצד נוכל לקבל שוב ממד שני? על ידי כיפוף קו ישר כך שייווצר שוב עיגול.
אם תדמיינו עיקול של שטח עגול, תחילה תקבלו קערה ולבסוף, אם תמשיכו לכופף אותו, הוא הופך לכדור. בדרך זו, קו מעוקל רוכש ממד שני ומשטח מעוקל ממד שלישי. ואם תוכלו לכופף קובייה, היא תצטרך להתעקל לתוך הממד הרביעי, התוצאה תהיה טסרקט כדורי.
שטח כדורי יכול להיחשב כמבנה דו ממדי מעוקל. בטבע הכדור מופיע בצורת תא, היצור החי הקטן ביותר. גבול התא הוא כדורי. כאן יש לנו את ההבדל בין חיים לחסר-חיים. מינרלים בצורתם הגבישית תמיד תחומים במשטחים שטוחים, בעוד שהחיים בנויים מתאים ולכן תחומים על ידי משטחים כדוריים. כשם שקריסטלים עשויים כדורים שהשתטחו, או מישורים, כך החיים עשויים מתאים או כדורים הסמוכים זה לזה. ההבדל בין חיים לחסר-חיים טמון באופי הגבולות שלהם. אוקטהדרון תחום בשמונה משולשים. אם נדמיין את שמונת צדדיו ככדורים, נקבל משהו חי המורכב משמונה פריטים (תאים).
אם "מעקלים" קובייה שהיא תלת ממדית, התוצאה היא היווצרות ארבעה ממדים, הטסרקט הכדורי. אך אם תעקלו את כל החלל, הצורה המתקבלת היא משהו שמתייחס לחלל התלת ממדי כמו כדור במישור. כשם שקובייה, כאובייקט תלת ממדי, תחומה על ידי משטחים מישוריים, כך כל גביש מוגבל על ידי מישורים. המהות של קריסטל היא זו התחומה על ידי משטחים שטוחים. תמצית החיים היא שהם בנויים ממשטחים מעוקלים, כלומר תאים, בעוד שצורה ברמת קיום גבוהה עוד יותר תהיה תחומה על ידי מבנים בעלי ארבעה ממדים. צורה תלת ממדית תחומה בצורות דו ממדיות. ישות בעלת ארבעה ממדים – כלומר יצור חי – תחומה על ידי ישויות תלת ממדיות, כדורים ותאים. ישות בעלת חמישה ממדים תחומה על ידי ישויות בעלות ארבעה ממדים, טסרקט כדורי. כך אנו מבינים שעלינו לעלות מישויות תלת ממדיות לישויות בעלות ארבעה ממדים ולאחר מכן לישויות בעלות חמישה ממדים.
אנו שואלים את עצמנו: מה חייב להופיע בישות בעלת ארבעה ממדים? חייב להיות שינוי בתוך הממד השלישי.[5] במילים אחרות, כאשר אתם תולים על הקיר תמונות דו-ממדיות, הן בדרך כלל נשארות ללא תנועה. כאשר אתם רואים תמונות דו ממדיות נעות, עליכם להסיק כי הסיבה לתנועה יכולה להיות רק מחוץ לפני השטח של הקיר – כלומר, הממד השלישי של החלל הוא זה שחולל את השינוי. כאשר אתם מגלים שינויים המתרחשים בממד השלישי, עליכם להסיק מכך כי לממד הרביעי יש השפעה על ישויות שעוברות שינויים בתוך שלושת ממדי החלל שלהן.
אנחנו לא באמת מזהים צמח כשאנחנו מכירים אותו רק בשלושת הממדים שלו. הצמחים משתנים כל הזמן. שינוי הוא היבט מהותי של הצמחים, תכונה של צורת קיום גבוהה יותר. קובייה נשארת ללא שינוי; צורתה משתנה רק כשאתם שוברים אותה. צמח משנה את צורתו בכוחות עצמו, דבר שפירושו שהשינוי חייב להיגרם על ידי גורם הקיים מחוץ לממד השלישי ומהווה ביטוי לממד הרביעי. מהו הגורם הזה?
אתם מבינים, אם יש לכם קובייה ותציירו אותה בזמנים שונים תגלו שהיא תמיד נשארת בעינה. אך כאשר אתם מציירים צמח ומשווים את הציור המקורי עם ציור נוסף שלכם כעבור שלושה שבועות, המקור השתנה. לכן האנלוגיה שלנו תקפה במלואה. כל יצור חי מצביע על יסוד גבוה יותר שבו ישותו האמיתית שוכנת, והזמן הוא הביטוי של יסוד עליון זה. הזמן הוא הביטוי הסימפטומטי של ביטוי החיים (נתפס כממד הרביעי) בשלושת הממדים של המרחב הפיזי. במילים אחרות, כל הישויות שלזמן יש משמעות פנימית עבורן הן דימויים של ישויות בעלות ארבעה ממדים. לאחר שלוש או ארבע שנים הקובייה תישאר בעינה. אולם שתיל השושנה משתנה מכיוון שלזמן יש משמעות אמיתית עבורו. מה שאנו רואים בשושנה הוא רק התמונה התלת ממדית של מהות השושנה, שהיא בעלת ארבעה ממדים. הזמן הוא דימוי או הטלה של הממד הרביעי, של החיים האורגניים, לתוך שלושת הממדים המרחביים של העולם הפיזי.
כדי להבהיר כיצד כל ממד עוקב מתייחס לקודמו, אנא חישבו על הדברים הבאים. לקובייה יש שלושה ממדים. כדי לדמיין את הממד השלישי אתם אומרים שהוא ניצב במאונך לממד השני והממד השני ניצב במאונך לממד הראשון. מה שמאפיין את שלושת הממדים זה שהם במאונך זה כלפי זה. אנו יכולים גם לחשוב על הממד השלישי כעולה מהממד הבא, הרביעי. תארו לעצמכם שהייתם צובעים את פני הקובייה ומתמרנים את הצבעים בצורה מסוימת, כפי שעשה הינטון. ניתן לבצע שינוי כזה והוא תואם בדיוק את השינויים שעוברת ישות תלת ממדית כשהיא מתפתחת עם הזמן לממד הרביעי. כאשר אתם חותכים ישות בעלת ארבעה ממדים בנקודה מסוימת- כלומר, אתם לוקחים את הממד הרביעי שלה – אתם הורסים את הישות. לעשות זאת לצמח זה כמו לקחת הטבעה של הצמח על ידי יציקתו בגבס. אתם אוחזים בו על ידי הרס הממד הרביעי, גורם הזמן, והתוצאה היא צורה תלת ממדית. כאשר לזמן, לממד הרביעי, יש חשיבות קריטית עבור ישות תלת ממדית מסוימת, פירוש הדבר שישות זו חייבת להיות חיה.
ועכשיו אנו מגיעים לממד החמישי. אפשר לומר שלממד זה צריך להיות גבול אחר, הניצב במאונך לממד הרביעי. ראינו שהיחס בין הממד הרביעי והשלישי דומה ליחס בין הממד השלישי לשני. הרבה יותר קשה לדמיין את הממד החמישי, אך אנחנו יכולים שוב להשתמש באנלוגיה כדי לקבל מושג אודות הדבר. כיצד מופיע כל ממד? כאשר אתה מצייר קו, לא מופיעים ממדים נוספים כל עוד הקו ממשיך באותו כיוון. ממד נוסף מתווסף רק כאשר תדמיינו שני זרמים או כוחות מנוגדים שנפגשים ומתאזנים בשלב מסוים. הממד החדש מופיע רק כביטוי לאיזון של כוחות. עלינו להיות מסוגלים לראות את הממד החדש כתוספת של קו שבו מתאזנים שני זרמי כוחות. אנו יכולים לדמיין את הממד מגיע מימין או משמאל, כחיובי במקרה הראשון ושלילי בשני. כך אני מבין כל ממד כזרם של כוחות קוטביים עם מרכיב חיובי ושלילי. איזון כוחות המרכיבים הקוטביים הוא הממד החדש.
אם ניקח זאת כנקודת מוצא, בואו נפתח תמונה של הממד החמישי. ראשית עלינו לדמיין את ההיבטים החיוביים והשליליים של הממד הרביעי שאנו יודעים שהוא ביטוי הזמן. בואו נדמיין התנגשות בין שתי ישויות שהזמן משמעותי עבורן. אז חייב להופיע כתוצאה מכך משהו דומה למה שקראנו בעבר עצירה של כוחות מנוגדים. כאשר שתי ישויות בעלות ארבעה ממדים יוצרות קשר, זהו הממד החמישי שלהם. הממד החמישי הוא תוצאה של החלפה או איזון של פעולת הכוחות הקוטביים שבאמצעותם שתי ישויות חיות שמשפיעות זו על זו מייצרות משהו שאין להן במשותף בשלושת הממדים הרגילים של החלל, וגם לא בממד הרביעי, בזמן. ליסוד החדש הזה יש גבולות מחוץ לממדים האלה. זה מה שאנו מכנים אמפתיה או רגש, היכולת של ישות אחת לדעת על האחרת. זוהי ההכרה בהיבט הפנימי (הרוחני-נפשי) של ישות אחרת. ללא הוספת הממד החמישי – כלומר, מבלי להיכנס לתחום הרגש – ישות לעולם לא תוכל לדעת דבר על ההיבטים של ישות אחרת, היבטים הנמצאים מחוץ לזמן ולחלל. כמובן שיש להבין את הרגש כאן רק כהשלכה או ביטוי של הממד החמישי בתוך העולם הפיזי.
יהיה קשה מדי לבנות את הממד השישי באותו אופן, אז בינתיים אני פשוט אגיד לכם מהו. אם נמשיך את אותו קו חשיבה היינו מוצאים כביטוי של הממד השישי משהו שהונח בעולם הפיזי התלת ממדי כמודעות עצמית. כישות תלת ממדית, יש לאדם, במשותף עם ישויות תלת ממדיות אחרות, את הפלסטיות של דימויו. לצמחים יש ממד נוסף, הרביעי. מסיבה זו לעולם לא תמצאו את ישותו האמיתית של הצמח בשלושת ממדי החלל. עליכם לעלות לממד הרביעי, אל התחום האסטרלי. אך אם תרצו להבין ישות חיה, עליכם לעלות לממד החמישי, לדווכאן התחתון או לתחום הרופה; ואם תרצו להבין ישות המודעת לעצמה, בני אדם, עליכם לעלות לממד השישי, לדווכאן העליון או לתחום הארופה. לפיכך, האיש שאנו פוגשים כיום הוא באמת ישות של שישה ממדים. מה שאנו מכנים רגש או אמפתיה ומודעות עצמית הם השלכות של הממד החמישי והשישי לחלל תלת ממדי רגיל. למרות שעל פי רוב באופן בלתי מודע, בני האדם מגיעים עד למישורים הרוחניים האלה; רק שם ניתן לזהות את טבעם האמיתי. ישויות בעלות שישה ממדים יכולות להגיע לידיעה אפילו של העולמות העליונים אם רק ינסו להיפטר מהמאפיין האמיתי של הממדים הנמוכים.
אני יכול רק להראות מדוע אנשים מאמינים שהעולם הוא תלת ממדי בלבד. תפיסתם מבוססת על התמונה שהעולם הוא רק השתקפות של גורמים גבוהים יותר. במראה אתה יכול לראות לכל היותר תמונת מראה של עצמך. למעשה, שלושת הממדים של המרחב הפיזי שלנו הם השתקפויות, תמונות חומריות של שלושה ממדים יצירתיים סיבתיים גבוהים יותר. כתוצאה מכך, לעולם החומרי שלנו יש מקביל רוחני קוטבי, בקבוצה של שלושת הממדים הגבוהים הבאים, כלומר הרביעי, החמישי והשישי. במובן דומה, לממדים שמעבר לקבוצת ממדים זו יש מקבילים קוטביים בעולמות רוחניים עוד יותר רחוקים, שהם מעבר להבנתנו.
חישבו על מים ועל מי קרח קפואים. בשני המקרים החומר זהה, אך למים ולקרח צורות שונות לחלוטין. אתם יכולים לדמיין תהליך דומה המתרחש בשלושת הממדים הגבוהים יותר של האדם. כאשר אתם מדמיים את האדם כישות רוחנית בלבד, עליכם לחשוב עליו כבעל רק שלושת הממדים הגבוהים יותר: מודעות עצמית, רגש וזמן, וכי שלושת הממדים הללו משתקפים בעולם הפיזי בשלושת הממדים הרגילים.
כשהיוגי (תלמיד האזוטריות) רוצה לגשת לידע של העולמות העליונים, עליו להחליף בהדרגה את ההשתקפויות במציאות. לדוגמה, כאשר הוא חושב על צמח עליו ללמוד להחליף את הממדים התחתונים בממדים העליונים. על ידי למידה להתעלם מאחד הממדים המרחביים של הצמח והחלפתו בממד הגבוה יותר המתאים – כלומר הזמן – הוא בסופו של דבר משיג תמונה של ישות דו ממדית בתנועה. מה עוד התלמיד צריך לעשות באזוטריות כדי שישות זו תישאר לא רק תמונה, אלא תתאים למציאות? אם הוא פשוט יתעלם מהממד השלישי ויוסיף את הרביעי, התוצאה תהיה אימגינציה. התמונה הבאה תעזור לנו להתקדם לעבר התשובה: על ידי צילום ישות חיה, גם אם נתחמק מהממד השלישי מאירועים שהיו בתחילה תלת ממדים, רצף התמונות מוסיף את ממד הזמן. אם לאחר מכן נוסיף את הרגש לתמונת האנימציה הזו אנו מבצעים פעולה הדומה לזו שתיארנו כעיקול מבנה תלת ממדי לממד הרביעי. התוצאה של פעולה זו היא צורה בעלת ארבעה ממדים שממדיה כוללים שניים מהממדים המרחביים הרגילים ושניים גבוהים יותר, כלומר זמן ורגש. ישויות כאלה אכן קיימות, ועכשיו, כשהגעתי למסקנה האמיתית של חקר הממדים, הייתי רוצה לציין אותם בפניכם.
תארו לעצמכם שני ממדים מרחביים – כלומר מישור – והניחו שמישור זה ניחן ביכולת תנועה. תארו לעצמכם שהוא מתעקל והופך להיות ישות הדוחפת לפניה משטח דו ממדי. ישות כזו חייבת לפעול בצורה שונה מאוד מישות תלת ממדית בחלל שלנו. הישות השטוחה שבנינו בצורה זו פתוחה לחלוטין בכיוון אחד. יש לה מראה דו ממדי; היא באה לקראתכם ואתם לא יכולים לעקוף אותה. ישות זו היא ישות זוהרת ואינה אלא פתיחות בכיוון אחד.
באמצעות ישות כזאת, המתקדשים מתוודעים לישויות אחרות, אותן הם מתארים כשליחים אלוהיים המתקרבים אליהם בלהבות אש. התיאור של משה שקיבל את עשרת הדיברות בהר סיני מראה כי התקרבה אליו ישות כזו וכי הוא היה יכול לתפוס את ממדיה. ישות זו, הדומה לאדם שהממד השלישי שלו נלקח, הייתה פעילה ברגש ובזמן.
דימויים מופשטים במסמכים דתיים אינם רק סמלים חיצוניים. הם מציאות כבירה שהאדם יכול לדעת על ידי שליטה במה שניסינו להבין באמצעות אנלוגיות. ככל שתתמסרו יותר בשקידה ובמרץ לבניית אנלוגיות כאלה, כך תשקעו בהן יותר, והן תפעלנה על רוחכם ותשחררנה יכולות גבוהות. זה חל, למשל, על ההסבר של האנלוגיה בין קובייה למשושה לבין זה שבין טסרקט לבין דודקאהדרון מעוין. האחרון מייצג את הטלת הטסרקט לעולם הפיזי התלת ממדי. כשמסתכלים על הצורות האלה כאילו יש להן חיים משל עצמן – כלומר, נאפשר לקובייה לצמוח אל מחוץ להטלה שלה, המשושה, ולטסרקט להתפתח אל מחוץ להטלה שלו, הדודקאהדרון המעוין – הגוף הנפשי התחתון שלכם לומד להבין את הישויות שתיארתי זה עתה. כאשר לא רק עקבתם אחר הצעותיי אלא גרמתם לכך שזה יתעורר לחיים, כפי שעושים תלמידים אזוטריים, במודעות מלאה בהקיץ, תבחינו כי צורות בעלות ארבעה ממדים תתחלנה להופיע בחלומותיכם. בשלב זה, אתם לא צריכים להרחיק לכת כדי להיות מסוגלים להביאן לתודעתכם בעירות. לאחר מכן תוכל לראות את הממד הרביעי בכל ישות בעלת ארבעה ממדים.
המישור האסטרלי הוא הממד הרביעי.
הדוואכן עד לרופה הוא הממד החמישי.
הדוואכן עד לארופה הוא הממד השישי.[6]
שלושת העולמות הללו – הפיזי, האסטרלי והשמיימי (דוואכן) – כוללים שישה ממדים. עולמות אפילו גבוהים יותר הם הפכים קוטביים של ממדים אלה.
מינרל צומח בעל חיים אדם
ארופה מודעות עצמית
רופה רגש מודעות עצמית
מישור אסטרלי חיים רגש מודעות עצמית
מישור פיזי צורה חיים רגש מודעות עצמית
צורה חיים רגש
צורה חיים
צורה
————————————————————————————
- ההתייחסות כאן היא ככל הנראה לספריו של הינטון 'רומנים מדעיים' [1886], 'עידן מחשבה חדש' [1900] ו-'הממד הרביעי' [1904]. ↑
- אפלטון, הרפובליקה, ספר 7, 514a-518c. לגבי שופנהאואר לא ניתן לקבוע היכן הוא משתמש במשל זה. ↑
- צולנר מפנה את תשומת הלב לפרשנות זו של האלגוריה של אפלטון על המערה בחיבורו Über Wirkungen in dir Ferne [1878a], עמוד 260. ↑
- עיין בהרצאה הראשונה בסדרה זו: 24 במרץ 1905. ↑
- שאר הטקסט של הרצאה זו כולל בתוכו שברי תרגומים המובאים בחיבורו של Haase [1916], שעזרו להבהיר את משמעותו. ↑
- בספרות התיאוסופית, שלושת האזורים העליונים של ארץ הרוח נקראים אזורי ארופה, בניגוד לארבעת האזורים התחתונים או רופה. ראו GA93a. בשאלת הממדיות בקשר עם המבנים או האזורים של עולם הרוח, ראו גם את הרצאתו של רודולף שטיינר מ-17 במאי 1905; שאלות ותשובות של 7 באפריל 1921 (GA76) ו-12 באפריל 1922 (GA82); הרצאות של 19, 20, 22 ו-26 באוגוסט 1923 (GA 227). ↑

