הממד הרביעי

רודולף שטיינר

GA324a

תרגום מרומנית: מ. ברכה

עריכת תרגום: דניאל זהבי

תיקונים: דליה דיימל

לספר ראו כאן

הרצאה מספר 7

חלל דו ממדי

7.11.1905 ברלין

לחלל הרגיל שלנו יש שלושה ממדים – אורך, רוחב ועומק. לקו יש רק ממד אחד, אורך. הלוח על הקיר הוא מישור, כלומר, יש לו שני ממדים, אורך ורוחב. לעצם מוצק יש שלושה ממדים. כיצד מופיעה צורה תלת ממדית?

דמיינו צורה ללא ממדים כלשהם, כלומר נקודה. יש לה אפס ממדים. כאשר נקודה נעה בכיוון קבוע, נוצר קו ישר או צורה חד ממדית. כעת דמיינו את הקו נע. התוצאה היא מישור עם אורך ורוחב. ולבסוף, מישור נע מתאר צורה תלת ממדית. עם זאת, לא נוכל להמשיך בתהליך זה על מנת להשיג על ידי תנועה של אובייקט תלת ממדי, התהוות ארבעה ממדים או ממד רביעי. כיצד נוכל להשתמש בתמונות כדי לפתח מושג לגבי הממד הרביעי? כמה מתמטיקאים ומדענים – צולנר, למשל – התפתו להביא את עולם הרוח להרמוניה עם עולם החושים שלנו בהנחה שעולם הרוח קיים בחלל בעל ארבע ממדים.^[1]

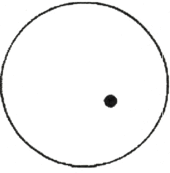$C:\Users\דניאל\AppData\Local\Microsoft\Windows\INetCache\Content.Word\001.bmp$ איור 46

תארו לעצמכם עיגול, צורה סגורה לחלוטין במישור. נניח שמישהו יבקש מאיתנו להזיז מטבע שמחוץ למעגל לתוכו (איור 46). עלינו לחתוך את היקף המעגל או – אם איננו רוצים לגעת בהיקף – להרים את המטבע לחלל ולהניח אותו בתוך המעגל, דבר שיחייב אותנו לעזוב את הממד השני ולהיכנס אל השלישי. על מנת להזיז את המטבע בצורה קסומה לתוך קובייה או כדור, עלינו לעזוב את הממד השלישי ולעבור דרך הממד הרביעי. הצלחתי להבין בחיים האלה את אופי החלל כשהתחלתי ללמוד גיאומטריה הטלית סינתטית מודרנית והבחנתי במשמעות שיש בשינוי המעגל לקו ישר (איור 47). העולם מתגלה במחשבות המעודנות ביותר של הנפש.^[2]

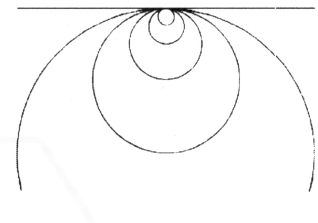$C:\Users\דניאל\AppData\Local\Microsoft\Windows\INetCache\Content.Word\001.bmp$ איור 47

ועכשיו בואו נדמיין עיגול. אנו יכולים לעקוב אחר היקפו ולחזור למקום בו התחלנו. תארו לעצמכם שהעיגול הולך וגדל עוד ועוד, בעוד שקו משיק נשאר קבוע. כשהעיגול הופך ליותר ויותר שטוח, הוא בסופו של דבר יהפוך לקו ישר. כשאני עוקב אחר העיגולים הגדלים יותר ויותר, אני תמיד יורד בצד אחד ועולה בחזרה בצד השני לפני שאחזור לנקודת ההתחלה. בסופו של דבר אני זז לכיוון אחד – נגיד ימינה – עד שאגיע לאינסוף. אז אני צריך לחזור מאינסוף מהצד השני, משמאל, מכיוון שרצף הנקודות בקו ישר מתנהג כמו עיגול. כך אנו רואים שלחלל אין סוף, כפי שלקו ישר אין קצה, מאחר ורצף הנקודות שלו זהה לאלו של עיגול סגור. בהתאם לכך, עלינו לדמיין את החלל האינסופי של המרחב כעומד בפני עצמו, בדיוק כפי שמשטח כדורי סגור בפני עצמו. תיארתי חלל אינסופי בעזרת עיגולים או כדורים. מושג זה יוביל אותנו לתפוס את מציאות החלל.^[3]

במקום לדמיין את עצמנו נעים לאינסוף ומסתובבים ללא שינוי מהכיוון השני, בואו נדמיין שאנו נושאים עימנו אור. כפי שהוא נראה מנקודה קבועה מימין הקו, האור הזוהר הופך להיות חלש יותר ויותר ככל שאנו מתרחקים, וחזק יותר ויותר ככל שאנו חוזרים איתו מאינסוף. אם נדמיין את השינויים בעוצמת האור כחיובי ושלילי, יש לנו את החיובי מצד אחד היכן שהאור מתחזק, ואת השלילי בצד שני. אנו מוצאים את שני הקטבים האלה, שהם פשוט ההשפעות הנגדיות של החלל, בכל ההשפעות של עולם הטבע. מחשבה זו מובילה למושג החלל כמשהו מלא כוח ולרעיון שהכוחות הפעילים בחלל אינם אלא ביטויים של כוח זה עצמו. כבר לא נפקפק באפשרות לגלות כוח הפועל בתוך חלל תלת ממדי, ונגיע לכך שכל התופעות המרחביות מבוססות על יחסים ממשיים בחלל.

יחסים שכאלו הם שזירת שני ממדים. כדי ליצור שתי טבעות שלובות זו בזו, עלינו לפתוח אחת מהן כדי להכניס את השנייה. כעת אשכנע את עצמי ברבגוניות הטבועה בחלל על ידי פיתול פעמיים צורה זו, רצועת נייר מלבנית, כלומר החזקת קצה אחד בחוזקה תוך כדי סיבוב הקצה השני ב-360 מעלות. לאחר מכן מהדקים את שני קצות הרצועה בעזרת סיכות. חיתוך הטבעת המפותלת הזו לחצי, לאורכה, גורם לשתי טבעות שזורות זו בזו שלא ניתן להפרידן מבלי לשבור אחת מהן. פשוט על ידי סיבוב הרצועה, אפשרנו ביצוע פעולה בתוך שלושת הממדים שאחרת ניתן לבצע רק על ידי כניסה לממד הרביעי. זה לא רק משחק; זוהי מציאות קוסמית. יש לנו את השמש, מסלול כדור הארץ סביב השמש ומסלול הירח סביב כדור הארץ (איור 48). מכיוון שכדור הארץ נע סביב השמש, מסלולי הירח וכדור הארץ שזורים זה בזה כמו שתי טבעות הנייר. במהלך האבולוציה של כדור הארץ, הירח התנתק מכדור הארץ. הפרדה זו התרחשה באותו אופן כמו ההשתלבות של שתי טבעות הנייר שלנו. כאשר אנו מסתכלים על החלל בצורה זו הוא הופך לחי באופן פנימי.

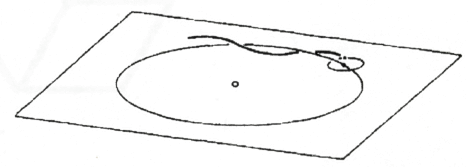$C:\Users\דניאל\AppData\Local\Microsoft\Windows\INetCache\Content.Word\001.bmp$ איור 48

הבא נחשוב על ריבוע. תארו לעצמכם שהוא נע בחלל עד שהוא יוצר קובייה. תנועת הריבוע חייבת להיות בניצב למיקומה ההתחלתי. קובייה מורכבת משישה ריבועים היוצרים את פני השטח שלה. כדי לתת לכם סקירה כללית של הקובייה אני יכול למקם את ששת הריבועים זה ליד זה במישור (איור 49). אני יכול לבנות מחדש את הקובייה על ידי הרמת הריבועים האלה כלפי מעלה, ובכך להעביר אותם לממד השלישי. הקובייה השישית מונחת מעל. כדי ליצור צורה זו, דמוית הצלב, פירקנו את הקובייה לשני ממדים. פרישת צורה תלת ממדית הופכת אותה לצורה דו ממדית.

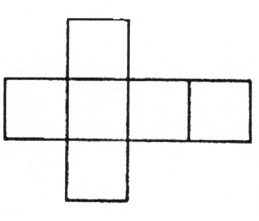$C:\Users\דניאל\AppData\Local\Microsoft\Windows\INetCache\Content.Word\001.bmp$ איור 49

כפי שאתם יכולים לראות, גבולותיה של קובייה הם ריבועים. קובייה תלת ממדית תמיד תחומה בריבועים דו ממדיים. בואו נסתכל על ריבוע אחד. הוא דו ממדי וגבולותיו הם ארבעה קטעים של קו חד ממדי. אני יכול למקם את ארבעת קטעי הקו האלה בממד אחד (איור 50). הקצוות המגדירים את אחד מממדי הריבוע מצוירים באדום עם קווים אחידים, והממד האחר נצבע בכחול ומצויר בקווים מנוקדים. במקום להגיד אורך ורוחב, אני יכול לדבר על הממד האדום והכחול.

$C:\Users\דניאל\AppData\Local\Microsoft\Windows\INetCache\Content.Word\001.bmp$ איור 50

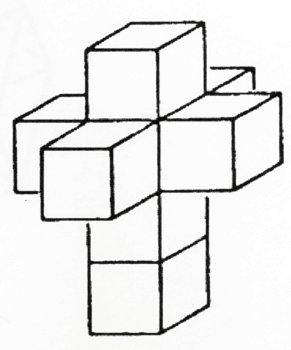
אני יכול לבנות מחדש את הקובייה משישה מרובעים. זה אומר שאני חורג מהמספר ארבע (מספר צלעות הריבוע), למספר שש (מספר המישורים היוצרים את פני הקובייה). אם נלך צעד אחד קדימה, אנו עוברים משש לשמונה (מספר הקוביות היוצרות את “הפנים” של צורה בעלת ארבעה ממדים). סידרנו את שמונה הקוביות הללו כך שיצרו את המקבילה התלת ממדית של הצורה הקודמת, המורכבת משישה ריבועים, במישור הדו ממדי (איור 51).

$C:\Users\דניאל\AppData\Local\Microsoft\Windows\INetCache\Content.Word\001.bmp$ איור 51

עכשיו תארו לעצמכם שאצליח להפוך מבנה זה מבפנים החוצה, לקפל אותו ולהרכיב אותו כך שהקובייה השמינית תכסה את כל המערך. אני משתמש בשמונה הקוביות ליצירת צורה בעלת ארבעה ממדים בחלל בעל ארבעה ממדים. הינטון מכנה צורה זאת טסרקט. גבולותיה מורכבים משמונה קוביות, כשם שגבולות הקובייה מורכבים משישה ריבועים. לפיכך, טסרקט של ארבעה ממדים תחום על ידי שמונה קוביות תלת ממדיות.

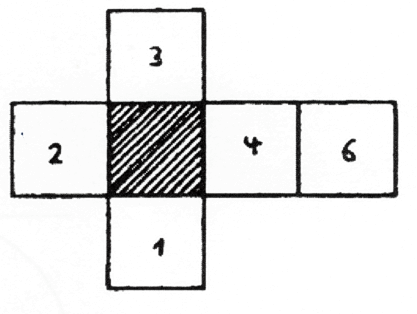
בואו נדמיין ישות שיכולה לראות רק בשני ממדים. כאשר היא מסתכלת על הריבועים הנפרשים של הקובייה, היא רואה רק את ריבועים 1, 2, 3, 4 ו-6, אך לעולם לא את ריבוע 5, זה המוצלל במרכז הצורה (איור 52). משהו דומה קורה לכם כשאתם מסתכלים על אובייקט בעל ארבעה ממדים שנפרש. מכיוון שאתם יכולים לראות אובייקטים תלת ממדיים בלבד, לעולם לא תוכלו לראות את הקובייה הנסתרת באמצע.

$C:\Users\דניאל\AppData\Local\Microsoft\Windows\INetCache\Content.Word\002.bmp$ איור 52

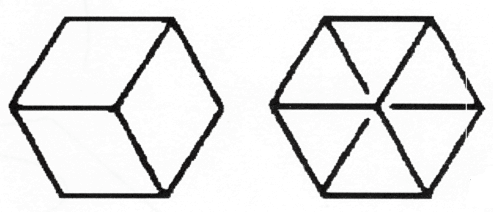
עכשיו דמיינו את הקובייה מצוירת בצורה כזו שקווי המתאר שלה מופיעים כמשושה. השאר מוסתר מאחור. מה שאתם רואים הוא תמונת צל, הטלה של הקובייה התלת ממדית בחלל דו ממדי (איור 53). תמונת הצל הדו ממדית של הקובייה התלת ממדית מורכבת ממעוינים, מקביליות דו-צדדיות. אם אתם מדמיינים את הקובייה כעשויה מחוט, תוכלו לראות גם את המעוינים האחוריים. הטלה זו מציגה שישה מעוינים חופפים. כך תוכלו להטיל את כל הקובייה לחלל דו ממדי.

$D:\Pictures\גכדגכג.BMP$ איור 53

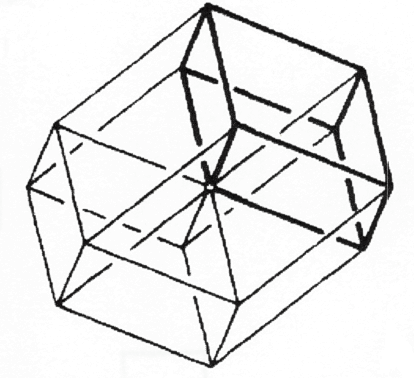
עכשיו דמיינו את הטסרקט שלנו שנוצר בחלל בעל ארבעה ממדים. על ידי הטלת צורה זו לחלל תלת ממדי עלינו להשיג ארבע קוביות מעוינות באלכסון (מקביליות) שאינן חופפות: את אחת מהקוביות המעוותות באלכסון נצייר כמו באיור 54.

$D:\Pictures\2021-10-15\002.BMP$ איור 54

עם זאת, שמונה קוביות מעוינות אלכסוניות כאלה צריכות לחדור זו בזו כדי לקבל תמונה תלת ממדית מלאה של טסרקט בעל ארבעה ממדים בחלל תלת ממדי. אנו יכולים לתאר בכך את הצל התלת ממדי השלם של טסרקט בעזרת שמונה קוביות מעוינות החודרות זו לזו. הצורה המרחבית המתקבלת היא תריסריון מעוין עם ארבעה אלכסונים מרחביים (איור 55). בדיוק כמו שבהטלה המעוינת של קובייה שלושה מעוינים סמוכים חופפים לשלושת האחרים, כך שרק שלוש מתוך שש פניה של הקובייה נראות, כך בהטלה של התריסריון המעוין של הטסרקט, רק ארבע קוביות מעוינות שאינן חודרות נראות לעין כמו הטלות של שמונה הקוביות הגבוליות של הטסרקט, שכן ארבע קוביות מעויינות סמוכות מכסות לחלוטין את ארבע האחרות.

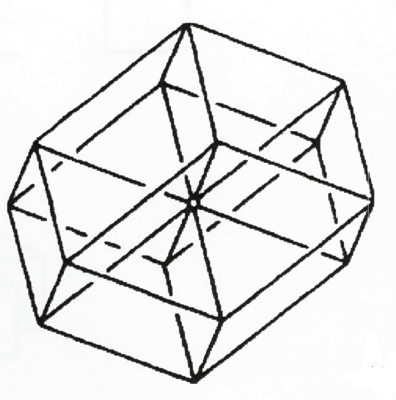$D:\Pictures\2021-10-15\003.BMP$ איור 55

כך אנו יכולים לבנות את הצל התלת ממדי של טסרקט, אם כי לא את האובייקט עצמו בעל ארבעת הממדים. כך אנו בעצמנו צללים של ישותנו בעלת הארבעה ממדים. כאשר אנו עוברים מהמישור הפיסי למישור האסטרלי עלינו לפתח את היכולת שלנו ליצור תמונות פנימיות. תארו לעצמכם ישות דו ממדית השואפת שוב ושוב לבנות באופן חי תמונת צל תלת ממדית שכזו. בנייה של תמונה פנימית כזו של היחס בין הממד השלישי לרביעי, יניע כוחות פנימיים שיאפשרו לכם להסתכל אל תוך החלל האמיתי, לא המתמטי, של ארבעת הממדים.

תמיד נישאר חסרי אונים בעולמות העליונים אם לא נפתח כוחות המאפשרים לנו לראות בעולמות העליונים כאן, בעולם התודעה הרגילה. העיניים בהן אנו משתמשים כדי לראות בעולם הפיזי הנתפס בחושים, מתפתחות כאשר אנו עדיין ברחם. כך עלינו לפתח איברים על-חושיים כאשר אנו עדיין נמצאים ברחם כדור הארץ, כדי שנוכל להיוולד בעולמות העליונים כרואים. התפתחות העין הפיזית כאשר אנו נמצאים ברחם היא דוגמה המאירה תהליך זה.

יש לבנות קובייה לפי ממדי האורך, הרוחב והגובה. יש לבנות טסרקט באמצעות אותם ממדים, בתוספת של ממד רביעי. ככל שצמח גדל, הוא יוצא מהחלל התלת ממדי. כל ישות שחיה בזמן משוחררת משלושת הממדים הרגילים. הזמן הוא הממד הרביעי. הוא נשאר בלתי נראה בשלושת הממדים של החלל הרגיל וניתן לראות אותו רק עם כוחות ראיה על-חושיים. נקודה נעה יוצרת קו, קו נע יוצר מישור, ומישור נע יוצר צורה תלת ממדית. כאשר חלל תלת ממדי נע, התוצאה היא צמיחה והתפתחות. אז יש לנו כאן, חלל בעל ארבעה ממדים, או זמן, המוקרן אל חלל תלת ממדי כתנועה, צמיחה והתפתחות.

תגלו שהמחשבות הגיאומטריות שלנו, איתן בנינו את שלושת הממדים הרגילים, נמשכות אל תוך החיים הרגילים. הזמן מאונך לשלושת הממדים ומהווה את הממד הרביעי. הוא גדל. כאשר הזמן מקבל חיות אצל ישות כלשהי, מופיעות יכולות חושיות. כאשר הזמן מוכפל בתוך הישות באופן שתנועה עצמית מתרחשת, התוצאה היא ישות חייתית בעלת חושים. במציאות, ישות כזו כוללת חמישה ממדים, ואילו לאדם יש שישה ממדים.

יש לנו ארבעה ממדים בתחום האתרי (המישור האסטרלי), חמישה ממדים בתחום האסטרלי (הדוואכן התחתון) ושישה ממדים בדוואכן העליון. כך נובעים גילויי הרוח השונים. כשהדוואכן מטיל את הצל שלו בחלל האסטרלי התוצאה היא הגוף האסטרלי שלנו. העולם האסטרלי המוטל כצל אל החלל האתרי נותן לנו את הגוף האתרי שלנו וכן הלאה.^[4]

עולם הטבע מת כשהזמן זז לכיוון אחד ומתחדש כשהזמן נע לכיוון השני. שתי הנקודות בהן נפגשים זרמים אלה הן לידה ומוות. העתיד מתקרב אלינו כל הזמן כדי לפגוש אותנו. אם החיים היו נעים רק בכיוון אחד, שום דבר חדש לא היה מופיע. לבני אדם יש גם רוח – כלומר העתיד שלהם, האינטואיציות שלהם הזורמות אליהם. העבר שפועל הוא הזרם שמגיע מהצד השני; הוא קובע את הישות כפי שהתפתחה עד כה.

————————————————————————————————-

ראו את הרצאותיו של שטיינר מ-24 ו-31 במרץ 1905. ↑
ראו את האוטוביוגרפיה של רודולף שטיינר, נתיב חיי (GA28), פרק ג’, [יצא לאור בעברית בהוצאת בדולח] והרצאתו מ-3 באפריל 1922 (GA82). ↑
בקטע זה, רודולף שטיינר מתייחס למישור הרחוק (או המוחלט) של החלל האוקלידי, וכתוצאה מכך לחלל היטלי. לחלל היטלי אין גבולות, כלומר, אנו יכולים לנסוע ל”אינסוף” לכל כיוון ואנו יכולים לפנות מהכיוון ההפוך. [הערת המתרגם לרומנית]. ↑
הדוואכן העליון והתחתון הם ממלכות שמיימיות שהנפש עוברת דרכם אחרי המוות. ראו את ספרו של רודולף שטיינר: גוף נפש רוח – יצא לאור בעברית בהוצאת מיכאל. ↑

הממד הרביעי – 07