הממד הרביעי

רודולף שטיינר

GA324a

תרגום מרומנית: מ. ברכה

עריכת תרגום: דניאל זהבי

תיקונים: דליה דיימל

לספר ראו כאן

הרצאה מספר 5

31.5.1905 ברלין

בפעם האחרונה ניסינו להשיג צורה של מבנה מרחבי בעל ארבעה ממדים על ידי צמצומו לשלושה ממדים. תחילה הפכנו צורה תלת מימדית לצורה דו ממדית. החלפנו את הממדים בצבעים, ובנינו את התמונה שלנו באמצעות שלושה צבעים לייצוג שלושת הממדים של הקובייה. לאחר מכן פרשנו את הקובייה באופן שכל המשטחים הונחו במישור, וכתוצאה מכך התקבלו שישה ריבועים שצדדיהם, בעלי הצבעים השונים, ייצגו את שלושת הממדים בחלל דו ממדי.

אחר כך דמיינו את המעבר של כל ריבוע של שטח הקובייה אל הממד השלישי, כך שהעברנו אותו בערפל צבעוני ואפשרנו לו להופיע שוב בצד השני. דמיינו את כל המשטחים המרובעים שנעים דרך ריבועי המעבר ונצבעים על ידם. כך השתמשנו בצבעים כדי לנסות להציג את הקובייה התלת ממדית בשני ממדים. כדי לייצג ריבועים בממד אחד השתמשנו בשני צבעים שונים לצדדיהם המשויכים; כדי לייצג קובייה דו ממדית השתמשנו בשלושה צבעים. הדגמת צורה בעלת ארבעה ממדים במרחב התלת ממדי דרשה צבע רביעי.

אחר כך דמיינו קובייה עם שלושה צבעי משטח שונים המקבילים לריבוע שלנו עם שני צבעי הקצה השונים. כל קובייה כזו נעה דרך קובייה בצבע רביעי; כלומר, היא נעלמה בתוך הממד או הצבע הרביעי. על פי האנלוגיה של הינטון, גרמנו לכל קוביית גבול לעבור דרך צבע רביעי ולהופיע שוב בצד השני בצבע המקורי שלה.

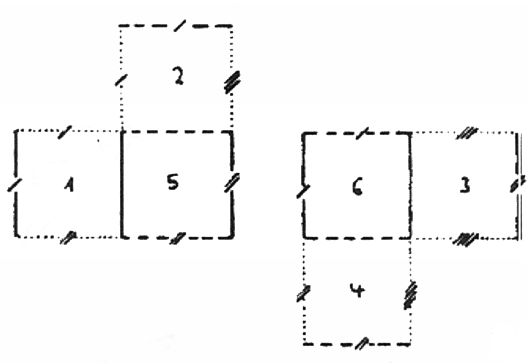$D:\Pictures\2021-10-09\001.BMP$ איור 31

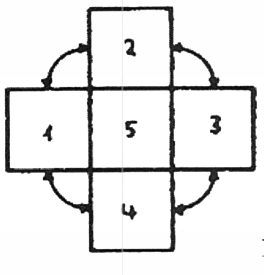
עכשיו אני רוצה לתת לכם אנלוגיה נוספת. נתחיל מחדש בהקטנת תלת ממד לשניים כהכנה לצמצום ארבעה ממדים לשלושה. עלינו לדמיין את בניית הקובייה משישה ריבועים, אך במקום להשאיר את כל הריבועים מחוברים כאשר נפרוס אותם במישור, נסדר אותם בצורה שונה, כפי שמוצג באיור 31. כפי שניתן לראות, חילקנו את הקובייה לשתי קבוצות של שלושה ריבועים כל אחת. שתי הקבוצות ממוקמות באותו מישור. עלינו להבין היכן ממוקמת כל קבוצה כאשר אנו מרכיבים את הקובייה מחדש. כדי להשלים מחדש את הקובייה אני צריך למקם קבוצה אחת על גבי השנייה כך שהריבוע 6 יהיה מעל הריבוע 5. ברגע שהריבוע 5 יהיה במקומו, עלי לקפל את הריבועים 1 ו-2 כלפי מעלה, בעוד שבריבועים 3 ו-4 מקופלים כלפי מטה (איור 32). לאחר מכן, הזוגות המתאימים למקטעים הליניאריים – כלומר בעלי אותו צבע (כאן עם אותו מספר וסוג חתכים, כפי שניתן לראות באיור 31) – יתחברו אז. קווים אלה המתפזרים בחלל הדו ממדי חופפים כאשר אנו עושים את המעבר למרחב התלת ממדי.

$C:\Users\דניאל\AppData\Local\Microsoft\Windows\INetCache\Content.Word\002.bmp$ איור 32

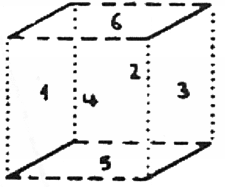
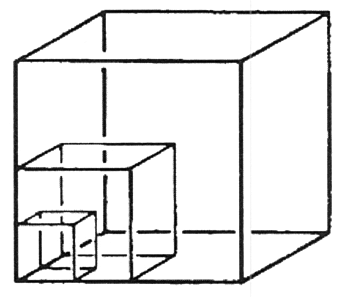
הריבוע מורכב מארבעה צדדים, קובייה מורכבת משישה ריבועים, וצורה בעלת ארבעה ממדים אמור להיות מורכבת משמונה קוביות. הינטון מכנה צורה זאת בעלת הארבעה ממדים טסרקט. המשימה להרכיב את שמונה הקוביות הללו ל"קובייה" אחת אינה פשוטה, לשם כך עלינו לגרום לכל אחת מהקוביות לעבור דרך הממד הרביעי. כשאני עושה עם הטסרקט את מה שעשיתי עם הקובייה, אני חייב לעקוב אחר אותו חוק. עלינו להשתמש באנלוגיה של היחס שבין צורה תלת ממדית למקבילה הדו ממדית שלה כדי לגלות את היחס בין צורה בעלת ארבעה ממדים למקבילה התלת ממדית שלה. במקרה של קובייה שנפרשה היו לנו שתי קבוצות של שלושה ריבועים. באופן דומה, על ידי פרישת טסרקט בעל ארבעה ממדים בחלל תלת ממדי, נוצרות שתי קבוצות של ארבע קוביות, שנראות כמו איור 33. השיטה של שמונה הקוביות היא גאונית מאוד.

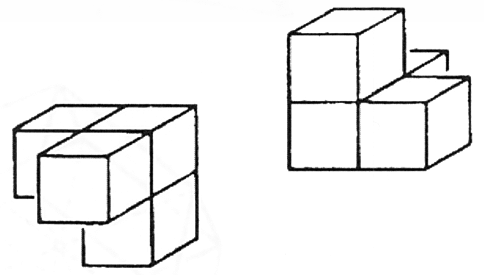$C:\Users\דניאל\AppData\Local\Microsoft\Windows\INetCache\Content.Word\002.bmp$ איור 33

עלינו לטפל בארבעה הקוביות בחלל תלת ממדי באותו אופן בו טיפלנו בריבועים בחלל דו ממדי. הסתכלו מקרוב על מה שעשיתי כאן. על ידי פרישת קובייה בחלל דו ממדי נוצרה קבוצה של שישה ריבועים. ביצוע פעולה דומה באמצעות טסרקט גורם למערכת של שמונה קוביות (איור 34). העברנו את ההשתקפויות שלנו מחלל תלת ממדי לחלל בעל ארבעה ממדים. חיבור הריבועים וחפיפת הקצוות בחלל התלת ממדי תואמים לקיפול הקוביות וחיבור משטחיהן בחלל בעל ארבעה ממדים. פרישת הקובייה בחלל דו ממדי הביאה לקווים מקבילים שחפפו זה את זה כששחזרנו את הקובייה. משהו דומה קורה עם משטחי הקוביות השונות של הטסרקט. על ידי פרישת טסרקט בחלל תלת ממדי, נוצרים המשטחים המתאימים של הקוביות המתאימות, אשר יחפפו מאוחר יותר. לפיכך, בטסרקט המשטח האופקי העליון של קובייה 1 נמצא באותו מישור כמו המשטח הקדמי של קובייה 5, כאשר אנו נעים אל הממד הרביעי.

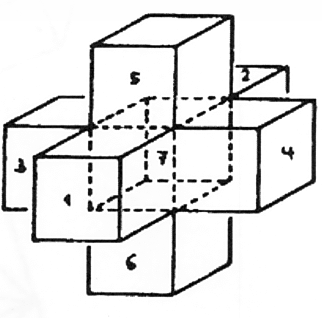$C:\Users\דניאל\AppData\Local\Microsoft\Windows\INetCache\Content.Word\002.bmp$ איור 34

באופן דומה, המשטח הימני של קובייה 1 עולה בקנה אחד עם המשטח הקדמי של קובייה 4, המשטח השמאלי של קובייה 1 עולה בקנה אחד עם המשטח הקדמי של קובייה 3 והמשטח התחתון של קובייה 1 עולה בקנה אחד עם המשטח הקדמי של קובייה 6. התאמות דומות קיימות עבור המשטחים האחרים. כאשר הפעולה הושלמה, הקובייה הנותרת היא קובייה 7, הקובייה הפנימית שהייתה מוקפת בשש הקוביות האחרות.^[1]

כפי שאתם יכולים לראות, שוב מדובר במציאת אנלוגיות בין הממד השלישי לרביעי. כפי שראינו באחת הצורות בהרצאה הקודמת, כשם שהריבוע החמישי, המוקף על ידי ארבעה ריבועים אחרים, נשאר בלתי נראה למי שיכול לראות רק בשני ממדים, כך גם לגבי הקובייה השביעית במקרה זה. היא נשארת מוסתרת מפני ראייה תלת ממדית. בטסרקט הקובייה השביעית הזו מתאימה לקובייה שמינית, המקבילה שלה בממד הרביעי.

כל האנלוגיות הללו משרתות אותנו כהכנה לממד הרביעי, שכן שום דבר בתפיסת החלל הרגילה שלנו לא מאלץ אותנו להוסיף ממדים אחרים לאלו שמוכרים לנו. בעקבות הדוגמה של הינטון, נוכל להשתמש בצבעים ולחשוב על הקוביות שהורכבו כך שהצבעים המתאימים נפגשים. ללא אנלוגיות שכאלה כמעט ואי אפשר לתת הדרכה כיצד עלינו להעלות צורה בעלת ארבעה ממדים.

ברצוני לדבר כעת על סוג אחר של ייצוג של גופים בעלי ארבעה ממדים בחלל תלת ממדי, שיכול לגרום לכם להבין טוב יותר מה הבעיה באמת. יש לנו אוקטהדרון^[2] בעל שמונה משטחים משולשים היוצרים ביניהם זוויות קהות (איור 35).

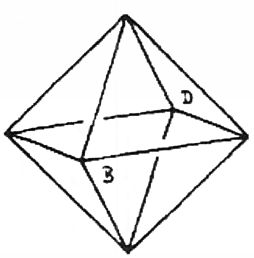$C:\Users\דניאל\AppData\Local\Microsoft\Windows\INetCache\Content.Word\001.bmp$ איור 35

אתם רואים, הקצוות האלה הם הצמתים של שני משטחים. לדוגמה, שניים מצטלבים לאורך AB ושניים לאורך EB. ההבדל היחיד בין אוקטהדרון לקובייה הוא הזווית שנוצרת על ידי הצטלבות המשטחים. כאשר המשטחים מצטלבים בזווית ישרה, כמו בקובייה, הצורה שנוצרת חייבת להיות קובייה. כשהן מצטלבות בזווית קהה, כפי שקורה כאן, נוצר אוקטהדרון. על ידי כך שהמשטחים מצטלבים בזוויות שונות אנו בונים צורות גיאומטריות אחרות.

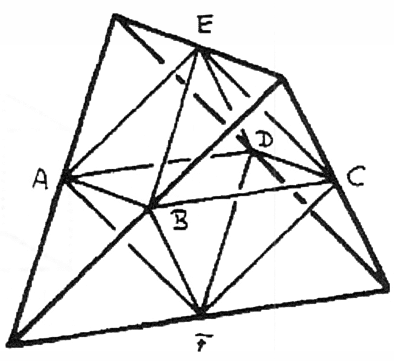$C:\Users\דניאל\AppData\Local\Microsoft\Windows\INetCache\Content.Word\001.bmp$ איור 36

בואו נדמיין דרך אחרת לגרום למשטחים של אוקטהדרון להצטלב. תארו לעצמכם שאחד המשטחים הללו, כגון AEB, מורחב לכל הכיוונים, וכי המשטח התחתון, BCF, ומשטחי ה-ADF ו-EDC מאחורי הצורה, מורחבים באופן דומה. גם המשטחים המורחבים האלה חייבים להצטלב, כלומר להצטלב לפי סימטריה כפולה. כאשר משטחים אלה מורחבים, נעלמים ארבעת המשטחים המקוריים האחרים של האוקטהדרון, ABF, EBC, EAD ו-DCF. מתוך שמונת המשטחים המקוריים נותרו רק ארבעה, וארבעה אלה יוצרים טטרהדרון שאפשר לקרוא לו גם חצי אוקטהדרון כי הוא מחצית משטחי האוקטהדרון המצטלבים. זה לא חצי אוקטהדרון במובן זה שהוא נחתך לשניים. כאשר שאר המשטחים של האוקטהדרון מורחבים עד שהם מצטלבים, הם יוצרים גם טטרהדרון. האוקטהדרון המקורי הוא צומת של שני הטטרהדרונים הללו. בסטריאומטריה או בקריסטלוגרפיה גיאומטרית, מה שנקרא חצי צורה הוא תוצאה של חציית מספר המשטחים במקום חלוקת הצורה המקורית לשניים.^[3] קל מאוד לדמיין זאת במקרה של אוקטהדרון. אם תדמיינו שקובייה חצויה באותו אופן וגורמת לאחד המשטחים להצטלב עם משטח אחר, תמיד תקבלו קובייה. חצי קובייה היא תמיד קובייה נוספת. ניתן להסיק מסקנה חשובה מתופעה זו, אך ראשית ברצוני להשתמש בדוגמה נוספת.^[4]

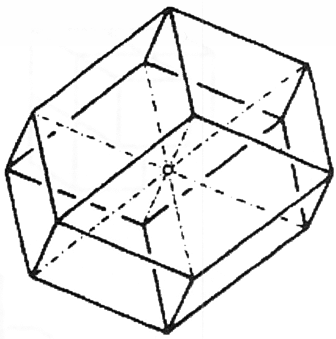$C:\Users\דניאל\AppData\Local\Microsoft\Windows\INetCache\Content.Word\001.bmp$ איור 37

יש לנו דודקהדרון [תריסרון] מעוין (איור 37). כפי שאתם יכולים לראות, משטחיו מצטלבים בזוויות מסוימות. יש לנו גם מערכת של ארבעה חוטים – אקרא להם חוטי ציר – הפונים לכיוונים שונים, כלומר הם אלכסונים המחברים פינות מנוגדות של התריסרון המעוין. חוטים אלה מייצגים את מערכת הצירים של התריסרון המעוין בדומה למערכת הצירים שניתן לדמיין בקובייה.

אנו משיגים קובייה עם מערכת של שלושה צירים אנכיים כאשר מתרחשת עצירה בכל אחד מאותם צירים, דבר היוצר משטחים מצטלבים. על ידי כך שהצירים מצטלבים בזוויות שונות, מתקבלות צורות גיאומטריות נוספות. למשל, הצירים של תריסרון מעוין מצטלבים בזוויות שאינן ישרות. זה נכון שבחצי קובייה נקבל קובייה נוספת, אך זה נכון רק לגבי קובייה. כאשר מספר משטחים של תריסרון מעוין נחצים, מתקבלת צורה מרחבית גיאומטרית שונה לחלוטין.

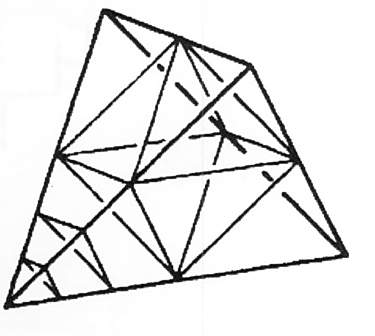$D:\Pictures\2021-10-09\001.BMP$ איור 38

ועכשיו בואו נסתכל כיצד אוקטהדרון מתייחס לטטרהדרון. תנו לי להראות לכם למה אני מתכוון. הקשר ניכר בבירור אם נהפוך בהדרגה אוקטהדרון לטטרהדרון. לשם כך, קחו טטרהדרון וחיתכו את אחד מקדקודיו, כפי שמוצג באיור 38. אנו ממשיכים לחתוך חלקים גדולים יותר ויותר עד שהקטעים מצטלבים בשולי הטטרהדרון. הצורה הנותרת היא אוקטהדרון. כשאני חותך את הקדקודים בזוויות מתאימות, הפכתי צורה מרחבית בת ארבעה מישורים לצורה בעלת שמונה צלעות.

$C:\Users\דניאל\AppData\Local\Microsoft\Windows\INetCache\Content.Word\002.bmp$ איור 39

מה שעשיתי עם טטרהדרון אי אפשר לעשות עם קובייה. לקובייה תכונות מיוחדות מאוד בכך שהיא מקבילה של מרחב תלת ממדי. תארו לעצמכם שכל החלל של היקום נבנה על ידי שלושה צירים אנכיים זה לזה. הכנסת מישורים אנכיים לשלושת הצירים האלה מייצרת תמיד קובייה (איור 39). לכן, בכל פעם שאנו משתמשים במונח קובייה, כדי לציין קובייה תיאורטית, אנו מדברים על הקובייה כמקבילה של מרחב תלת ממדי. כשם שהטטרהדרון הוא מקבילו של אוקטהדרון על ידי הרחבת מחצית צדדי האוקטהדרון עד שהם מצטלבים, כך גם קובייה בודדת היא המקבילה של החלל כולו.^[5] אם תדמיינו את כל החלל כחיובי, אז הקובייה תהייה שלילית. הקובייה היא הקוטב הנגדי של החלל כולו. הקובייה הפיזית היא הצורה הגיאומטרית המקבילה למעשה לכל החלל.

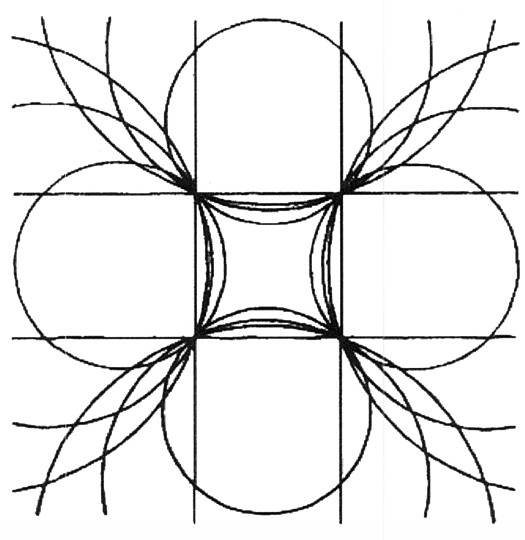
נניח שבמקום חלל תלת ממדי המוגבל על ידי מישורים דו ממדיים יש לנו חלל התחום על ידי שישה כדורים שהם צורות תלת ממדיות. אני מתחיל בהגדרת חלל דו ממדי בעזרת ארבעה עיגולים מצטלבים, כלומר, צורות דו ממדיות. עכשיו דמיינו שהמעגלים האלה הולכים וגדלים; כלומר, הקוטר שלהם גדל יותר ויותר והמרכזים שלהם הולכים ומתרחקים. עם הזמן, העיגולים יהפכו לקווים ישרים (איור 40). ואז במקום ארבעה עיגולים, יש לנו ארבעה קווים ישרים מצטלבים וריבוע.

$C:\Users\דניאל\AppData\Local\Microsoft\Windows\INetCache\Content.Word\002.bmp$ איור 40

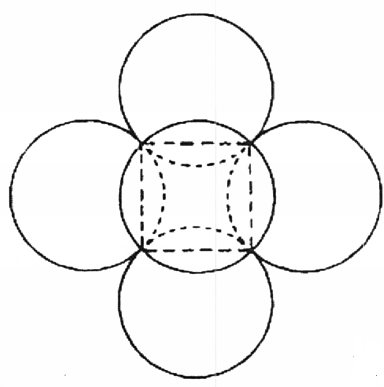
כעת, במקום עיגולים, דמיינו שישה כדורים היוצרים משהו הדומה לאוכמנית (איור 41). תארו לעצמכם שהכדורים הולכים וגדלים, ממש כמו העיגולים. בסופו של דבר, כדורים אלה הופכים למישורים שמגדירים קובייה, בדיוק כפי שהעיגולים הפכו לקווים המגדירים ריבוע. קובייה זו היא תוצאה של שישה כדורים שהפכו שטוחים. לכן, הקובייה היא מקרה מסוים של הצטלבות שישה כדורים, בדיוק כפי שהריבוע הוא מקרה מיוחד של הצטלבות של ארבעה עיגולים מושטחים.

$D:\Pictures\2021-10-09\002.BMP$ איור 41

כאשר מבינים בבירור שששת הכדורים הללו שהשתטחו למישורים התואמים את הריבועים בהם השתמשנו קודם לכן כדי להגדיר את הקובייה – כלומר, כאשר מדמיינים צורה כדורית שהופכת למישור שטוח – מקבלים את הצורה המרחבית התלת ממדית הפשוטה ביותר. ניתן לדמיין את הקובייה כתוצאה מהשטחה של שישה כדורים מצטלבים.

אנו יכולים לומר שנקודה במעגל חייבת לעבור דרך הממד השני כדי להגיע לנקודה נוספת במעגל. אך אם המעגל הפך כה גדול עד שהוא יוצר קו ישר, כל נקודה במעגל יכולה להגיע לכל נקודה אחרת על ידי מעבר דרך הממד הראשון בלבד.

חישבו על ריבוע המוגבל על ידי צורות דו ממדיות. כל עוד ארבע הצורות המגדירות את הריבוע הן עיגולים, הן דו ממדיות. ברגע שהן הפכו לקווים ישרים הן חד ממדיות.

המישורים המגדירים קובייה מתפתחים מצורות תלת ממדיות (כדורים) בכך שממד אחד מסולק מכל אחד מששת הכדורים. נראה כי משטחים אלה נפרשים על ידי הקטנת גודלם משלושה לשניים. כך הם הקריבו ממד. הם נכנסים לממד השני על ידי הקרבת ממד העומק. לכן נוכל לומר שכל ממד בחלל מתהווה על ידי הקרבה של הממד העליון הבא.

אם יש לנו צורה תלת ממדית עם גבולות דו ממדיים ובכך צומצמו הצורות התלת ממדיות לשני ממדים, עלינו להסיק מכך שאם נחשוב על מרחב תלת ממדי עלינו לחשוב על כל כיוון כגרסה השטוחה של מעגל אינסופי. ואז, אם ננוע בכיוון אחד, בסופו של דבר היינו חוזרים לנקודת ההתחלה בכיוון ההפוך. לפיכך, כל ממד רגיל של החלל הופיע על ידי איבוד הממד הגבוה הבא. מערכת תלת צירית טבועה בחלל התלת ממדי שלנו. כל אחד משלושת הצירים האנכיים הקריב את הממד הבא כדי להפוך לישר.

בדרך זו אנו מקבלים אפוא את המרחב התלת ממדי על ידי השטחת כל אחד משלושת הכיוונים הציריים. על ידי היפוך התהליך, כל אלמנט של החלל יכול גם להתעקל שוב. אז תתקבל סדרת המחשבות הבאה: כאשר אתה מכופף מבנה חד ממדי הצורה המתקבלת היא דו ממדית; צורה דו ממדית מכופפת הופכת לתלת ממדית. ולבסוף, על ידי כיפוף צורה תלת ממדית מתקבלת צורה בעלת ארבעה ממדים. כך ניתן לדמיין חלל בעל ארבעה ממדים כחלל מכופף תלת ממדי.

בשלב זה נוכל לבצע את המעבר מהמתים לחיים. בכיפוף זה תוכלו למצוא צורות מרחביות החושפות את המעבר הזה מהמתים לחיים. במעבר לתלת ממד, אנו מוצאים דוגמה מיוחדת של חלל בעל ארבעה ממדים; הוא נעשה שטוח. עבור התודעה האנושית, המוות אינו אלא כיפוף של התלת ממד לארבעה הממדים. באשר לגוף הפיזי עצמו, הדברים הפוכים: המוות הוא השטחה של ארבעה ממדים לשלושה.

————————————————————————————————————-

המצב המתואר כאן תואם לאיור 34א, במקרה של קובייה שנפרשת במישור: $C:\Users\דניאל\AppData\Local\Microsoft\Windows\INetCache\Content.Word\003.bmp$ איור 34א
לא ניתן לתאר את המיקום של ריבוע 6, ישירות מעל ריבוע 5 ישירות במישור. הצד העליון של ריבוע 2, הצד התחתון של ריבוע 4 והצד הימני והשמאלי של ריבועים 3 ו-1 חייבים להיראות זהים לדפנות ריבוע 6. בהתאם לכך, קוביות 7 ו-8 "חופפות" ואינן ניתנות להבחנה באופן ישיר במרחב תלת מימדי. המשטחים התחתונים והעליונים של קוביות 5 ו-6 בהתאמה, מימין ומשמאל של קוביות 3 ו-4 בהתאמה והחלק הקדמי והאחורי של קוביות 1 ו-2 בהתאמה, מהוות גם משטחים של קובייה 8. פרישת קובייה מקלה על כך. התבוננו בתיאום בין קצוות הריבוע השישי לאלו של הריבועים השכנים (איור 34ב).
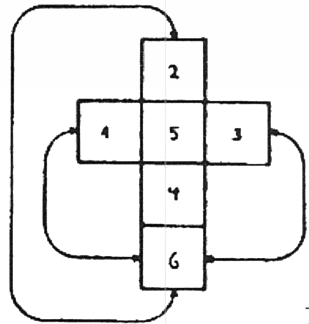$C:\Users\דניאל\AppData\Local\Microsoft\Windows\INetCache\Content.Word\003.bmp$ איור 34ב
איור 34ג מציג את המצב המקביל במקרה של טסרקט. יש לראות את משטחי הקובייה השמינית זהים למשטחי הקוביות השכנות.
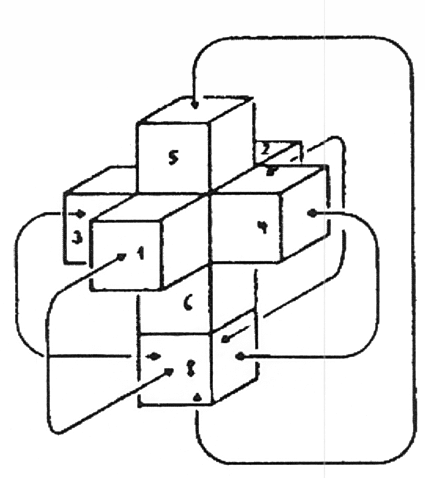$C:\Users\דניאל\AppData\Local\Microsoft\Windows\INetCache\Content.Word\003.bmp$ ↑איור 34ג
אוקטהדרון – תְּמָנְיוֹן משוכלל, הוא פאון בעל 8 פאות משולשות שוות צלעות, 6 קודקודים ו-12 מקצועות. ↑
רודולף שטיינר מתייחס כאן לנוהל סטנדרטי בקריסטלוגרפיה גיאומטרית. ↑
בקובייה כל זוג משטחים מנותקים מצטלבים בזווית ישרה. לא משנה באיזה משטחים אנו בוחרים, ומרחיבים אותם, תמיד נקבל, בצמתים, זוויות ישרות. בכל מקרה, בקובייה, על ידי צמצום מספר המשטחים, כבר לא מתקבל פולידרון סגור. ↑
ראו גם הרצאתו של שטיינר מ-31 במרץ 1905 [הרצאה מספר 2 בספר זה]. בלי קשר לשלושה מתוך ששת המישורים שנבחרו, התוצאה של הרחבתם לחלל היא "צורה" הנמתחת עד אינסוף. אם שלושת המשטחים שנבחרו אנכיים זה לזה, התוצאה היא צורה גיאומטרית המורכבת משלושה צירים אנכיים ושלושה מישורים המכילים אותם שניים על שניים. ניתן לראות דמות כזו כמייצגת את המרחב האוקלידי התלת ממדי והיא גם הבסיס הגיאומטרי של כל מערכת קואורדינטות אוקלידית או קרטזית. ↑

הממד הרביעי – 05

הממד הרביעי

רודולף שטיינר

לספר ראו כאן

כתיבת תגובה לבטל