הממד הרביעי

רודולף שטיינר

GA324a

תרגום מרומנית: מ. ברכה

עריכת תרגום: דניאל זהבי

תיקונים: דליה דיימל

לספר ראו כאן

הרצאה מספר 2

31.3.1905 ברלין

היום אדון בהיבטים בסיסיים ברעיון המרחב הרב-ממדי בהתייחסות מיוחדת לצ'ארלס הינטון, איש חכם מאוד.^[1] כזכור, בפעם האחרונה התחלנו באפס ממד והגענו לחלל רב-ממדי. הרשו לי לסכם בקצרה את הרעיונות לגבי מרחבים דו-ממדיים ותלת-ממדיים. מה הכוונה ביחסים סימטריים? כיצד אוכל להפגיש זו עם זו שתי צורות מישוריות סימטריות, כפי שהן הצורה האדומה הזו והכחולה הזו?

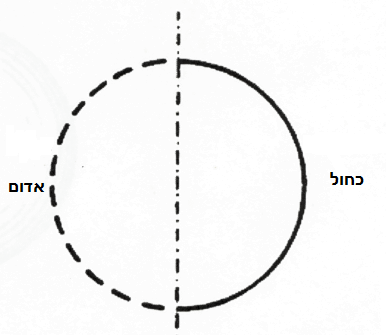$D:\Pictures\001.BMP$ איור 10

קל יחסית לעשות זאת עם שני חצאי עיגול. אני פשוט מכניס את האדום לכחול על ידי סיבובו (זהו סיבוב סביב מרכז המעגל שגורם לאחד מחצאי העיגולים "להחליק" מעל השני) (איור 10). אבל זה לא פשוט עם תמונות המראה למטה (איור 11). לא משנה איך אנסה להכניס את החלק האדום לחלק הכחול, אני לא יכול לגרום להם לחפיפה על ידי שהייה בתוך המישור. יש דרך להשיג זאת על ידי עזיבת המישור, כלומר הממד השני, ולהשתמש בממד השלישי, במילים אחרות אם נניח את הצורה הכחולה על האדום על ידי סיבובו בחלל סביב ציר הסימטריה.

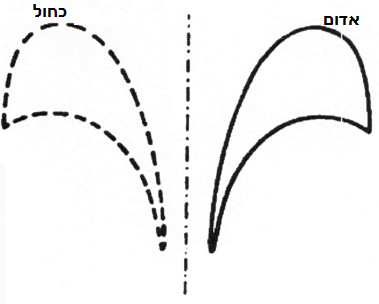$D:\Pictures\001.BMP$ איור 11

המצב דומה לזה של זוג הכפפות. אנחנו לא יכולים לגרום להן להתאים אחת לשנייה מבלי לעזוב את המרחב התלת ממדי. עלינו להיכנס לממד הרביעי.

בפעם הקודמת אמרתי שאם אנחנו רוצים לקבל מושג על הממד הרביעי, עלינו לאפשר ליחסים המרחביים להישאר זורמים כדי לייצר נסיבות דומות לאלה הקיימות כאשר אנו מבצעים את המעבר מהממד השני לממד השלישי: יצרנו צורות מרחביות משולבות מרצועות נייר וראינו שזה מביא לסיבוכים מסוימים. זה לא רק משחק, כי השתלבויות כאלה מתרחשות בכל מקום בטבע, במיוחד במקרה של תנועות שלובות של אובייקטים חומריים. תנועות אלה כוללות כוחות וגם הכוחות כרוכים זה בזה. קחו למשל את תנועת כדור הארץ סביב השמש ביחס לתנועת הירח סביב כדור הארץ. הירח מתאר מעגל המסתובב סביב מסלול כדור הארץ מסביב לשמש; כלומר, הירח מתאר ספירלה סביב מעגל. בשל תנועת השמש עצמה, הירח מבצע תנועה ספירלית נוספת סביבה, והתוצאה מכך היא קווי כוח מסובכים מאוד המשתרעים ברחבי החלל.

היחסים בין גופים שמיימיים דומים לרצועות הנייר המפותלות של סימוני שהראתי בפעם האחרונה. כפי שאמרתי קודם, עלינו להבין שאנו מתמודדים עם מושגים מרחביים מסובכים שאנו יכולים להבין אותם רק אם איננו מאפשרים להם להיות נוקשים. אם ברצוננו להבין את טבעו של המרחב, עלינו לתפוס אותו תחילה כבלתי נייד ואז לאפשר לו להיות נזיל שוב. זה כמו ללכת עד לאפס, שם אנו מוצאים את המהות החיה של נקודה.

בואו נסתכל שוב על אופן בניית הממדים. נקודה היא בעלת אפס ממדים, קו הוא חד-ממדי, משטח הוא דו-ממדי, ואובייקט מוצק הוא תלת-ממדי. לפיכך לקובייה יש שלושה ממדים: גובה, רוחב ועומק. כיצד צורות מרחביות בגדלים שונים מתייחסות זו לזו? תאר לעצמך שאתה קו ישר. יש לך רק גודל אחד ואתה יכול לנוע לאורך קו אחד בלבד. אם ישות כזאת היתה קיימת, מה יהיה רעיון המרחב שלה? היא לא היתה מסוגלת לתפוס את החד-מימדיות שלה. לאן שהיא תלך היא תוכל לדמיין רק נקודות כי הן כל מה שאנחנו יכולים לצייר תוך שהייה בתוך הקו הישר. ישות דו-ממדית תפגוש רק קווים, כלומר היא תתפוס רק ישויות חד-ממדיות.

ישות תלת-ממדית כגון קובייה, למשל, תתפוס ישויות דו-ממדיות אך לא את תלת הממדיות שלה. בני אדם יכולים לתפוס את תלת הממדיות שלהם. אם נסיק את המסקנה הנכונה עלינו להבין שאם ישות חד-ממדית יכולה לתפוס נקודות בלבד, ישות דו-ממדית רק קווים ישרים וישות תלת-ממדית רק משטחים, אז ישות שתופסת שלושה ממדים חייבת להיות בעלת ארבעה ממדים. העובדה שאנו יכולים לתחום ישויות חיצוניות בתלת-ממד ולתפעל מרחבים תלת-ממדים פירושה שאנו עצמנו חייבים להיות בעלי ארבעה ממדים. כשם שקובייה תוכל לתפוס רק שני ממדים ולא את התלת-ממד של עצמה, ברור שאיננו יכולים לתפוס את הממד הרביעי בו אנו חיים. כך מבינים שהאדם חייב להיות בעל ארבעה ממדים. אנו צפים על פני ים של הממד הרביעי כמו קרח על פני המים.

נחזור לדיון שלנו אודות בבואות-מראה (איור 11). קו אנכי זה מייצג חתך רוחב שנוצר על ידי מראה. המראה משקפת תמונה של הצורה משמאל. תהליך ההשתקפות מצביע מעבר לממד השני, לשלישי. כדי להבין את הקשר הישיר, ללא הפרעה, של בבואת-המראה עם המקור עלינו להניח שישנו ממד שלישי בנוסף לראשון ולשני.

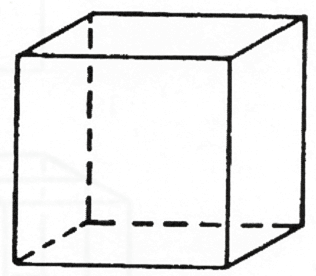$C:\Users\דניאל\AppData\Local\Microsoft\Windows\INetCache\Content.Word\001.bmp$ איור 12

הבה נבחן כעת את הקשר בין החלל החיצוני לבין התפיסה הפנימית. קובייה מחוצה לי נראית לי כתפיסה פנימית בתוכי (איור 12). המושג שלי לגבי הקובייה מתייחס לקובייה עצמה כתמונה המשקפת את המקור. המנגנון החושי שלנו משרטט דימוי של הקובייה. אם אנו רוצים לגרום לצורה הזאת להיות בחפיפה עם הקובייה המקורית עלינו לעבור דרך הממד הרביעי. כשם שתהליך שיקוף דו-ממדי חייב לעבור דרך הממד השלישי, כך גם המנגנון החושי שלנו חייב להיות בעל ארבעה ממדים על מנת שנוכל ליצור קשר ישיר בין דימוי מנטלי לאובייקט חיצוני. אם היית רואה רק בשני ממדים, היית מתמודד רק עם דימוי חלומי. לא היה לך מושג שקיים אובייקט אמיתי בעולם החיצון. כאשר אנו מדמיינים אובייקט, אנו מרחיבים את יכולת הדימוי המנטלי שלנו ישירות על אובייקטים חיצוניים דרך מרחב בעל ארבעה ממדים.

במצב האסטרלי בתקופות המוקדמות של האבולוציה של בני אדם הם היו רק חולמים. התמונות היחידות שהופיעו בתודעה שלנו אז, היו רק תמונות חלום.^[2] מאוחר יותר אנשים עשו את המעבר מהשלב האסטרלי לזה של המרחב הפיזי. בכך הגדרנו את המעבר מקיום אסטרלי לפיזי, חומרי, במונחים מתמטיים; לפני המעבר הזה, אנשים אסטרליים היו יצורים תלת ממדיים, כך שהם לא יכלו להרחיב את הדימויים המנטליים הדו ממדיים שלהם לעולם האובייקטיבי, החומרי, התלת ממדי. כאשר בני אדם הפכו ליצורים פיזיים, חומריים, הם רכשו את הממד הרביעי ולכן הצליחו לחוות חיים בשלושה ממדים.

המבנה הייחודי של המנגנון החושי שלנו מאפשר לנו להתאים את הדימויים המנטליים שלנו עם אובייקטים חיצוניים. בהתייחסות להתאמה של הדימויים המנטליים שלנו לאובייקטים חיצוניים, אנו עוברים דרך חלל בעל ארבעה ממדים, ומניחים את הדימוי המנטלי על פני האובייקט החיצוני. איך היו נראים הדברים מהצד השני אם היינו יכולים להיכנס לתוכם ולהסתכל עליהם משם? לשם כך עלינו לעבור דרך הממד הרביעי. העולם האסטרלי עצמו אינו עולם בעל ארבעה ממדים. אולם כשתופסים אותו יחד עם ההשתקפות שלו בעולם הפיזי, הוא בעל ארבעה-ממדים. כאשר אנו מסוגלים להסתכל על העולם האסטרלי והפיזי בו זמנית, אז אנו קיימים בחלל בעל ארבעה ממדים. הקשר של העולם הפיזי שלנו עם העולם האסטרלי הוא בעל ארבעה ממדים.

עלינו ללמוד להבין את ההבדל בין נקודה לכדור. במציאות, נקודה כפי שהיא מתוארת כאן אינה פסיבית, אלא מקרינה אור לכל הכיוונים (איור 13).

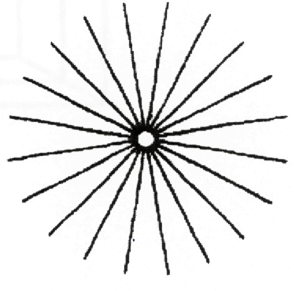$C:\Users\דניאל\AppData\Local\Microsoft\Windows\INetCache\Content.Word\001.bmp$ איור 13

מה יהיה ההיפך מנקודה כזו? בדיוק כמו שההיפך מקו שיוצא מימין לשמאל הוא קו משמאל לימין, לנקודה שמקרינה אור יש גם היפוך. תארו לעצמכם כדור ענק, כדור גדול ואינסופי המקרין חשיכה פנימה מכל הצדדים (איור 14). הכדור הזה מהופך לנקודה שמקרינה אור.

$C:\Users\דניאל\AppData\Local\Microsoft\Windows\INetCache\Content.Word\002.bmp$ איור 14

ההיפך האמיתי מנקודה שמקרינה אור הוא מרחב אינסופי שאינו חשוך באופן פסיבי, אלא באופן פעיל מציף את החלל בחשיכה מכל הכיוונים. מקור החושך ומקור האור הפוכים. אנו יודעים שקו ישר שנעלם עד אינסוף חוזר לאותה נקודה מהצד השני. באופן דומה, כאשר נקודה מקרינה אור לכל הכיוונים, האור חוזר מאינסוף כהיפוכו, כחשיכה.

ועכשיו נתבונן במקרה ההפוך. ראו את הנקודה כמקור לחשיכה. ההיפך שלה הוא מרחב שמקרין אור פנימה מכל הכיוונים. כפי שהסברנו בהרצאה הקודמת, נקודה הנעה לאורך קו אינה נעלמת לאינסוף, אלא חוזרת מהצד השני (איור 15).

$D:\Pictures\002.BMP$ איור 15

באופן דומה, נקודה המתרחבת או מקרינה אינה נעלמת לאינסוף אלא חוזרת מהאינסוף בצורה של כדור. הכדור הוא ההיפך מנקודה. החלל שוכן בנקודה. הנקודה היא ההיפך מהחלל.

מה ההיפך מקובייה? שום דבר מלבד סך המרחב האינסופי מינוס החלק שתופסת הקובייה. עלינו לדמיין את הקובייה מורכבת ממרחב אינסופי פלוס ההיפך שלה. איננו יכולים להימנע מקוטביות כאשר אנו מנסים לדמיין את עולמנו במונחים של כוחות דינאמיים. רק הקוטביות נותנת לנו גישה לחיים הטבועים באובייקטים.

כאשר האוקולטיסטים רואים קובייה אדומה, שאר החלל ירוק מכיוון שאדום הוא הצבע המשלים לירוק. לאוקולטיסט אין דימויים מנטליים פשוטים, העומדים בפני עצמם. הדימויים המנטליים שלו חיים ואינם אובייקטים מתים. הדימויים המנטליים שלנו מתים, בעוד שהעצמים בעולם חיים. כאשר אנו סומכים על הדימויים המנטליים המופשטים שלנו, איננו סומכים על העצמים עצמם. כאשר אנו מדמיינים כוכב שמקרין אור, עלינו לדמיין גם את התמונה ההפוכה שלו – כלומר מרחב אינסופי – בצבע המשלים המתאים. כשאנו עושים תרגילים כאלה אנו יכולים לאמן את החשיבה שלנו ולצבור ביטחון כיצד אנו יכולים לדמיין את הממדים שלנו.

אתם יודעים שריבוע הוא שטח דו-ממדי. ריבוע המורכב משני ריבועים אדומים ושני כחולים (איור 16) הוא משטח המקרין לכיוונים שונים בדרכים שונות. היכולת להקרין לכיוונים שונים היא יכולת תלת ממדית. כך יש לנו כאן את שלושת הממדים של אורך, רוחב ויכולת הקרינה.

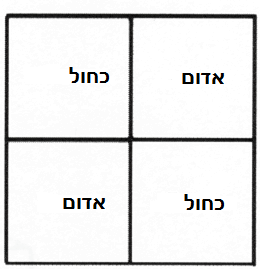$D:\Pictures\2021-10-03\002.BMP$ איור 16

את מה שעשינו כאן עם משטח אפשר לעשות גם עם קובייה. כמו שהריבוע למעלה מורכב מארבעה ריבועי משנה, אנו מדמיינים קובייה המורכבת משמונה קוביות משנה (איור 17). בהתחלה, לקובייה יש שלושה ממדים: גובה, רוחב ועומק. בנוסף עלינו להבחין ביכולת מסוימת להקרין אור בתוך כל אחת מקוביות המשנה. התוצאה היא ממד נוסף, היכולת להקרין, אותו יש להוסיף לגובה, לרוחב ולעומק.

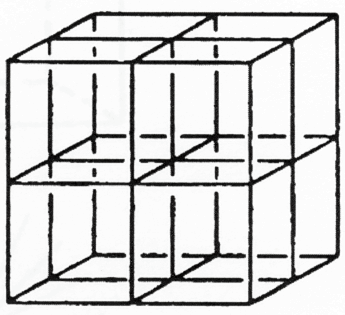$C:\Users\דניאל\AppData\Local\Microsoft\Windows\INetCache\Content.Word\002.bmp$ איור 17

אם לכל אחת משמונה קוביות המשנה יש יכולת קרינה שונה, אז אם יש לי רק קובייה אחת עם היכולת שלה להקרין באופן חד-צדדי ואני רוצה לקבל קובייה שתקרין לכל הכיוונים, אני חייב להוסיף אחת לכל הכיוונים, להכפיל אותו עם ניגודיו – ולכן עלי לחבר אותו ל-16 קוביות.^[3]

בפעם הבאה שניפגש נלמד כיצד לדמיין חללים רב ממדים.

————————————————————————————

צ'ארלס האוורד הינטון (1853-1907 Charles Howard Hinton), מתמטיקאי וסופר. הינטון הושפע מאוד מאביו, ג'יימס הינטון (1822-1875), מנתח שכתב גם מאמרים, כולל כמה על אמנות החשיבה שבה הוא דחה כל מגבלה מלאכותית על חשיבה או התנסות בתקנות התנהגותיות דתיות, חברתיות או משפטיות.
חיפוש הוודאות גרם להינטון למשבר חמור בשנת 1875. הוא נקט ברעיון שרק סידור החפצים בחלל יכול להוביל לידע ודאי בהחלט. בעיסוקו בתרגילי חשיבה בנוגע לסידור הקובייה המחולקת לקוביות קטנות יותר, הוא ניסה להשתחרר מכל המגבלות הסובייקטיביות שהוטלו, כגון מושגי "למעלה" ו"למטה". תוך כדי כך, הוא נתקל בבעיה של חלוקת תמונת המראה של שתי קוביות ותהה אם לא ניתן להוכיח שתופעה זו נקבעת באופן סובייקטיבי. בעת שחקר סוגיה זו, הוא גילה מסה של פרידריך צולנר על הממד הרביעי [1878 Friedrich Zöllner] במאמר זה, מציג זולנר בקצרה את ניסוייו ודעותיו לגבי מציאות הממד הרביעי.
הינטון בילה את שארית חייו בחקר בעיית הממד הרביעי. הוא למד את המעבר מהמימד השני לממד השלישי בדרכים שונות ליצירת בסיס איתן לתיאור הממד הרביעי במרחב התלת-ממדי המורגש. בפרט הוא פיתח תרגילים שיטתיים לרכישת תפיסה עקבית של מרחב תלת-ממדי, ולמשך זמן מה שמר על הדעה שאפשר באותה מידה לרכוש תפיסה של מרחב ארבע-ממדי. הינטון האמין כי העולם כולל הרחבה חומרית בממד הרביעי וניסה להוכיח השערה זו באמצעות התנסויות שונות בפסיכולוגיה ובפיזיקה. תפיסה זו נתקלה בהתנגדות הן מצד מטריאליסטים שקיבלו את קיומם של שלושה ממדים בלבד והן מצד ספיריטואליסטים שהעדיפו לפרש את הממד הרביעי כבעל אופי רוחני בלבד. הינטון היה כותב שנוי במחלוקת שנקרא בכבוד רב על ידי קהל חילוני, במיוחד על ידי תיאוסופים ואמנים אוונגרדיים, אך הוא נדחה או התעלמו ממנו בחוגים אקדמיים. ↑
ראו רודולף שטיינר, 'מדע הנסתר בקוויו העיקריים' (GA13), פרק ד': "האדם והתפתחות העולם". ↑
[הערת המתרגם לרומנית]: פשוט לא ניתן לשחזר את כוונתו של שטיינר באנלוגיה זו, ואין ביצירתו של הינטון דבר המתאים לרעיונות מסוג זה. למרות שגם הינטון משתמש בצבעים כדי להמחיש את המעבר מהממד השני לממד השלישי ובעיקר את המעבר מהממד השלישי לרביעי, הוא משתמש בהם בצורה שונה מאוד. בהרצאה של שטיינר ב-24 במאי 1905, הוא מסכם מחדש את מחשבותיו של הינטון בנושא.
הבסיס הגיאומטרי של מחשבותיו של שטיינר, המוצג כאן, הוא זה: קטע של קו המחולק לשניים ניתן להפוך לריבוע המאפשר לכל מחצית הקטע להיות הצד המשותף של שני ריבועים סמוכים קטנים יותר. התוצאה היא ריבוע גדול יותר המחולק לארבעה ריבועים קטנים יותר (איור 16). ניתן לבנות קובייה המחולקת לשמונה קוביות קטנות יותר על ידי מתן אפשרות לכל ריבוע קטן להפוך למשטח: צמוד לשתי קוביות סמוכות (איור 17). הדמות התלת-ממדית המתאימה, הקובייה הארבע-ממדית, נובעת כאשר כל אחת משמונה הקוביות הקטנות יותר של הקובייה התלת-ממדית מתפרשת כגבול המשותף של שתי קוביות ארבע-ממדיות. התוצאה היא קובייה בת ארבעה ממדים המחולקת ל-16 קוביות ארבע-ממדיות. ↑

הממד הרביעי – 02

הממד הרביעי

רודולף שטיינר

לספר ראו כאן

כתיבת תגובה לבטל