הממד הרביעי
רודולף שטיינר
GA324a
תרגום מרומנית: מ. ברכה
עריכת תרגום: דניאל זהבי
תיקונים: דליה דיימל
לספר ראו כאן
הרצאה מספר 4
24.5.1905 ברלין
בהרצאה הקודמת ניסיתי לפתח רעיון סכמטי לגבי מרחב בעל ארבעה ממדים, דבר שמאוד קשה לעשות אם לא נשתמש באנלוגיה כתמונה של מרחב זה. הבעיה שאנו מתמודדים איתה היא כיצד להדגים צורה בעלת ארבעה ממדים כאן במרחב התלת ממדי שהוא סוג החלל היחיד שנגיש לנו בהתחלה. כדי לקשר את היסוד הלא מוכר של מרחב בעל ארבעה ממדים למשהו שאנו מכירים עלינו להביא אובייקט בעל ארבעה ממדים אל שלושה ממדים, כפי שהבאנו אובייקט תלת ממדי אל שני ממדים. ברצוני להשתמש בשיטתו של מר הינטון כדי להדגים בצורה ברורה ככל האפשר את הפיתרון לבעיית הייצוג של מרחב בעל ארבעה ממדים בתוך תלת מימד.
הרשו לי להתחיל ולהראות כיצד ניתן להכניס מרחב תלת ממדי לחלל דו ממדי. הלוח שלנו הוא משטח דו ממדי. כשנוסיף עומק לממדי הגובה והרוחב שלו נקבל מרחב תלת ממדי. עכשיו ננסה לתאר באופן אינטואיטיבי צורה תלת ממדית על הלוח הזה.
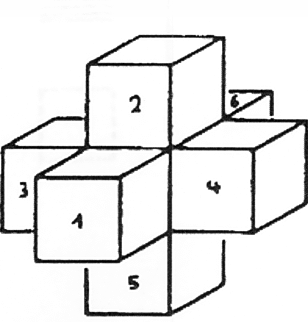
הקובייה היא צורה תלת ממדית מכיוון שיש לה גובה, רוחב ועומק. בואו ננסה להכניס קובייה זו לחלל דו ממדי, כלומר למישור. נוכל לקחת קובייה ולפרוש אותה כך שששת הצדדים המרובעים שלה יתפרסו במישור (איור 25). באופן זה יכולתי לדמיין את המשטחים התוחמים את הקובייה כפרושים בצורת צלב.
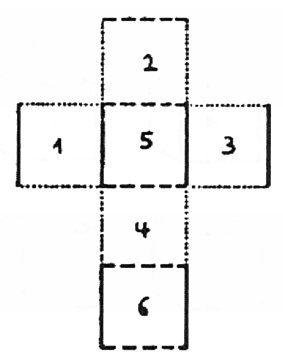 איור 25
איור 25
ששת הריבועים האלה יוצרים שוב קובייה אם אני מקפל אותם שוב כך שריבועים 1 ו-3, 2 ו-4, 5 ו-6 יהיו במיקומים מנוגדים. זוהי דרך פשוטה להעביר צורה תלת ממדית למישור.
איננו יכולים להשתמש בשיטה זו ישירות כאשר אנו רוצים לצייר את הממד הרביעי במרחב התלת ממדי. לשם כך נזדקק לאנלוגיה נוספת. נצטרך להשתמש בצבעים. אצבע את הצדדים של ששת הריבועים באופן שונה כך שזוגות מנוגדים של ריבועים יהיו באותו צבע. לריבועים 1 ו-3 אכין זוג צדדים אדומים (קווים מנוקדים) ואת הזוג האחר בצבע כחול (קווים אחידים). כמו כן אצבע את כל הקצוות האופקיים של יתר הריבועים בכחול ואת האנכיים באדום (איור 26).
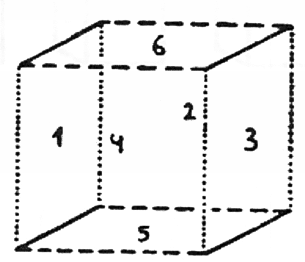 איור 26
איור 26
הסתכלו על שני הריבועים האלה, 1 ו-3. שני הגדלים שלהם מיוצגים על ידי שני צבעים, אדום וכחול. עבורנו, על הלוח האנכי שבו ריבוע 2 הוא אדום פירושו גובה, וכחול פירושו עומק. השתמשו בעקביות באדום לגובה ובכחול לעומק, הוסף ירוק (קווים מקווקווים) עבור רוחב, הממד השלישי והשלימו את פרישת הקובייה. לריבוע 5 יש צדדים כחולים וירוקים וכך גם ריבוע 6. עדיין יש ריבועים 2 ו-4. כשתדמיינו אותם פרושים, תגלו שהצדדים שלהם אדומים וירוקים.
בדימוי הקצוות הצבעוניים הללו, תבינו שהפכנו את שלושת הממדים לשלושה צבעים. במקום גובה, רוחב ועומק אנו קוראים להם אדום (מנוקד), ירוק (מקווקו) וכחול (קו מלא). שלושת הצבעים הללו מחליפים ומייצגים את שלושת ממדי החלל. עכשיו דמיינו את כל הקובייה מקופלת שוב. תוכלו להסביר את הוספת הממד השלישי בכך שהריבוע הכחול-אדום עבר דרך צבע ירוק, כלומר, משמאל לימין באיור 26. המעבר דרך הירוק או ההיעלמות בתוך הממד של הצבע השלישי, הוא המעבר דרך הממד השלישי.
תארו לעצמכם כי ערפל ירוק צובע את הריבועים האדומים-כחולים, כך ששני הקצוות (אדום וכחול) נצבעים. הקצה הירוק הופך לכחול-ירוק והקצה האדום מקבל גוון עכור. שני הקצוות מופיעים מחדש בצבעים שלהם רק במקום שהירוק נפסק. אני יכול לעשות את אותו הדבר עם ריבועים 2 ו-4, ולאפשר לריבוע אדום-ירוק לנוע דרך חלל כחול. אתם יכולים לעשות דבר דומה עם שני הריבועים הכחולים-ירוקים, 5 ו-6, על ידי הזזת אחד מהם דרך אדום. בכל אחד מהמקרים, הריבוע נעלם בצד אחד ושוקע בצבע אחר הצובע אותו עד שהוא מופיע מהצד השני בצבעו המקורי. לפיכך, שלושת הצבעים המוצבים בזווית ישרה זה לזה הם ייצוגים סימטריים של הקובייה שלנו. פשוט השתמשתי בצבעים לשלושת הממדים. על מנת לדמיין את השינויים שעוברים שלושת זוגות המשטחים של הקובייה, אנו מדמיינים שהם עוברים דרך ירוק, אדום וכחול, בהתאמה.
במקום הקווים הצבעוניים האלה דמיינו ריבועים, ובמקום חלל ריק דמיינו ריבועים בכל מקום. אז אני יכול לצייר את כל הצורה באופן אחר (איור 27). הריבוע שדרכו עוברים האחרים צבוע בכחול והשניים שעוברים דרכו – לפני ואחרי שהם עושים את המעבר – משורטטים לצידו. כאן הם באדום וירוק. בשלב הבא, הריבועים הכחולים-ירוקים עוברים דרך הריבוע האדום, ובשלב השלישי שני הריבועים האדומים-כחולים עוברים דרך הירוק.
 איור 27
איור 27
כאן רואים סוג נוסף של השטחת הקובייה. מתוך תשעת הריבועים המסודרים כאן, רק שישה – השורה העליונה והשורה התחתונה – יוצרים את פני הקובייה עצמה (איור 27). שלושת הריבועים האחרים בשורה האמצעית הם מעברים; משמעותם היא פשוט ששני הצבעים האחרים נעלמים בשלישי. כך, בקשר לתנועת המעבר, עלינו לקחת שני ממדים בבת אחת מכיוון שכל אחד מהריבועים הללו בשורה העליונה והתחתונה עשוי משני צבעים ונעלם בצבע שאינו מכיל אותם. אנו גורמים לריבועי הצבע האלה להיעלם בצבע השלישי שיופיע שוב בצד השני. הריבועים האדומים-כחולים עוברים דרך ירוק. לריבועים האדומים-ירוקים אין צדדים כחולים, ולכן הם נעלמים בכחול, בעוד שהריבועים הכחולים-ירוקים עוברים דרך אדום. כפי שתוכלו לראות, אנו יכולים לבנות את הקובייה שלנו מריבועים דו ממדיים – כלומר דו צבעוניים – שעוברים דרך ממד או צבע, שלישי.[1]
השלב המתבקש הבא הוא לדמיין קוביות במקום ריבועים ולדמיין את הקוביות הללו כמורכבות מריבועים בעלי שלושה צבעים (ממדים), כפי שבנינו את הריבועים מקווים דו צבעוניים. שלושת הצבעים תואמים את שלושת ממדי החלל. אם ברצוננו להמשיך כפי שעשינו עם הריבועים, עלינו להוסיף צבע רביעי, כך שכל קובייה תיעלם דרך הצבע שהיא חסרה. פשוט יש לנו ארבע קוביות מעבר בצבעים שונים – כחול, לבן, ירוק ואדום – במקום שלושה ריבועי מעבר. במקום ריבועים שעוברים דרך ריבועים יש לנו עכשיו קוביות שעוברות דרך קוביות. בדגמים של מר סכאוטן משתמשים בקוביות צבעוניות כאלו.
בדיוק כפי שגרמנו לריבוע אחד לעבור דרך ריבוע אחר, כעת עלינו לגרום לקובייה אחת לעבור דרך קובייה נוספת של הצבע שאין לה. לפיכך, הקובייה הלבנה-אדומה-ירוקה עוברת דרך קובייה כחולה. מצד אחד היא טובלת בתוך הצבע הרביעי ומופיעה שוב בצד השני בצבעה המקורי (איור 28.1). כך יש לנו כאן צבע או ממד אחד, התחום על ידי שתי קוביות שלמשטחים שלהן יש שלושה צבעים שונים.
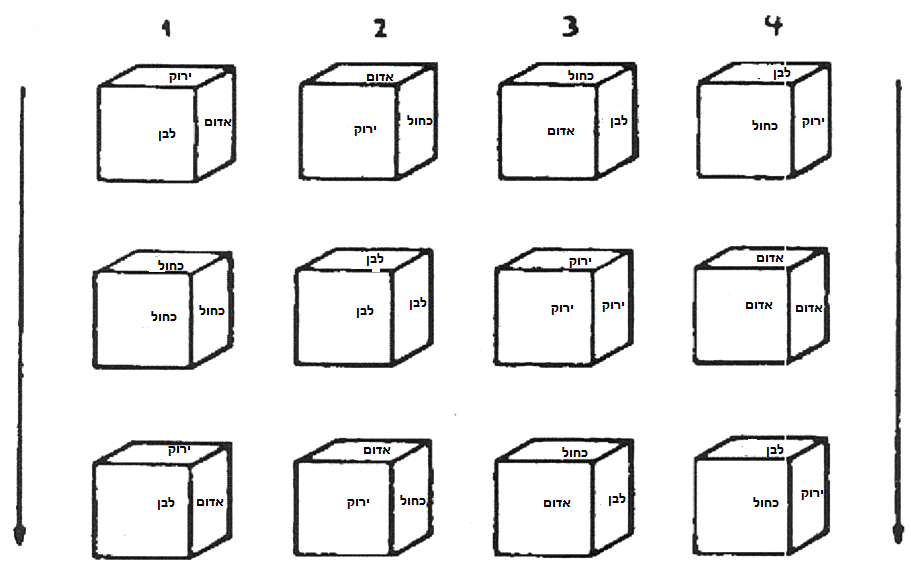 ציור 28
ציור 28
באופן דומה, עלינו לגרום כעת לקובייה הירוקה-כחולה-אדומה לעבור דרך הקובייה הלבנה (איור 28.2). הקובייה הכחולה-אדומה-לבנה עוברת דרך הירוקה (איור 28.3), ובאיור האחרון (איור 28.4) הקובייה הכחולה-ירוקה-לבנה חייבת לעבור בממד האדום; כלומר, כל קובייה חייבת להיעלם בצבע החסר שלה ולהופיע שוב בצד השני בצבעיה המקוריים.
ארבע הקוביות הללו מתייחסות זו לזו באותו אופן כמו שלושת הריבועים בדוגמה הקודמת. אנו זקוקים לשישה ריבועים כדי לתחום את גבולות הקובייה. אנו זקוקים גם לשמונה קוביות כדי ליצור את גבולות הצורה המקבילה בעלת ארבעת הממדים, הטסרקט. במקרה של קובייה נזקקנו לשלושה ריבועים נוספים המסמנים את ההיעלמות דרך הממד הנותר. הטסרקט דורש בסך הכל 12 קוביות המתייחסות זו לזו באותו אופן כמו תשעת הריבועים במישור. עשינו כעת עם הקובייה את מה שעשינו עם ששת הריבועים בדוגמה הקודמת. בכל פעם שבחרתי בצבע חדש הוספתי ממד חדש. השתמשנו בצבעים כדי לייצג את ארבעת הכיוונים המשולבים בצורה בעלת ארבעה ממדים. לכל אחת מהקוביות בצורה זו יש שלושה צבעים והיא עוברת דרך הצבע הרביעי.
המשמעות של החלפת ממדים בצבעים היא שכל עוד אנו דבקים בשלושת הממדים החדשים איננו יכולים פשוט להכניס אותם למישור דו ממדי. אבל באמצעות שלושה צבעים זה הופך להיות אפשרי. אנו עושים את אותו הדבר עם ארבעה ממדים כאשר אנו משתמשים בארבעה צבעים כדי ליצור בבואה בחלל תלת ממדי. זוהי אחת הדרכים להציג את הנושא המסובך הזה. הינטון השתמש בשיטה זו כדי לפתור את הבעיה בייצוג צורות בעלות ארבעה ממדים בתלת ממד.
בשלב הבא ארצה לפרוש שוב את הקובייה ולמקם אותה במישור. אני אצייר את זה על הלוח. לעת עתה, התעלמו מהריבוע התחתון באיור 25 ודמיינו שאתם יכולים לראות רק בשני ממדים – כלומר, לראות רק מה שניתן למצוא על פני שטח הלוח. במצב זה הנחנו חמישה ריבועים, כך שאחד מהם נמצא באמצע. השטח הפנימי נשאר בלתי נראה (איור 29). ניתן להסתובב מסביב, אך מכיוון שאתם יכולים לראות רק בשני ממדים, לא תראו את הריבוע ה-5.
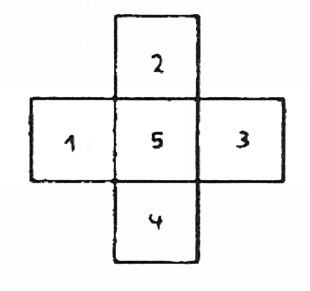 איור 29
איור 29
כעת, במקום לקחת חמישה מתוך ששת הריבועים של הקובייה, עשו את אותו הדבר עם שבע מתוך שמונה הקוביות היוצרות את גבולות הטסרקט, ופורשות בחלל את הצורה בעלת ארבעת הממדים. המיקום של שבע הקוביות מקביל לזה של משטחי הקובייה הנפרשים במישור הלוח, אך כעת יש לנו קוביות במקום ריבועים. הצורה התלת ממדית המתקבלת מקבילה למבנה צלב דו ממדי העשוי ריבועים והיא מקבילה שלו במרחב התלת ממדי. הקובייה השביעית, כמו אחד הריבועים, אינה נראית מכל מקום שאנו מביטים בה. לא ניתן לראות אותה על ידי ישות המסוגלת לראות רק בתלת ממד (איור 30). אם נוכל לקפל את הצורה הזו, כפי שאנו יכולים עם ששת הריבועים המקופלים של הקובייה, נוכל לעבור מהממד השלישי לממד הרביעי. הראינו כיצד ניתן ליצור ייצוג של תהליך זה באמצעות מעברי צבע.[2]
 איור 30
איור 30
הדגמנו לפחות כיצד אנו בני האדם, יכולים לדמיין מרחב בעל ארבעה ממדים, למרות העובדה שאנו תופסים רק בשלושה ממדים. מכיוון שאולי אתם תוהים כיצד אנו משיגים מושג לגבי חלל אמיתי בעל ארבעה ממדים, הייתי רוצה לעורר אתכם למיסתורין האלכימיה, כיוון שמבט אמיתי על מרחב בעל ארבעה ממדים קשור למה שהאלכימאים מכנים טרנספורמציה.
אם אנחנו רוצים לקבל מבט אמיתי על המרחב בעל הארבעה ממדים עלינו לבצע תרגילים מדויקים מאוד. עלינו קודם כל ליצור ראייה מאוד ברורה ועמוקה – ולא דימוי מנטלי – של מה שאנו מכנים מים. קשה להשיג ראיה כזו הדורשת מדיטציות ארוכות. עלינו לצלול לאופי המים בדיוק רב. עלינו לזחול לתוך טבע המים. כתרגיל שני עלינו ליצור ראיה של טבע האור. למרות שהאור מוכר לנו, אנו מכירים אותו רק בצורה בה אנו מקבלים אותו מבחוץ. באמצעות מדיטציה אנו רוכשים את מקבילו הפנימי של האור החיצוני, אנו לומדים מהיכן וכיצד בא האור; אנו בעצמנו מסוגלים לייצר משהו כמו אור. באמצעות מדיטציה, יוגים או תלמידים אזוטריים מקבלים את היכולת לייצר אור. אלה שבאמת עושים מדיטציה על מושגים טהורים, נותנים למושגים אלה לפעול על נפשם במהלך מדיטציה, או החשיבה נטולת החושים, אזי מפציע אור מתוך הרעיונות. הסביבה כולה נראית להם כאור זורם. תלמידי האזוטריות חייבים "לשלב באופן אלכימי" את ראיית המים שהם טיפחו עם ראיית האור. מים שחדורים לחלוטין באור הם מה שכינו האלכימאים מרקורי.
בשפת האלכימיה, מים בתוספת אור שווים למרקורי. במסורת האלכימית מרקורי הוא לא רק כספית רגילה. לאחר שהתעוררה היכולת שלנו ליצור אור מהעבודה שלנו עם מושגים טהורים, מרקורי מופיע כתערובת של אור זה עם ראיית המים שלנו. אנו משתלטים על הכוח של המים הללו החודרים באור, שהוא אחד ממרכיבי העולם האסטרלי.
היסוד השני מתעורר כאשר אנו מטפחים ראיית אוויר, כפי שלפני כן טיפחנו ראיית מים. באמצעות תהליך רוחני אנו מלקטים את תמצית כוח האוויר. לאחר מכן, על ידי ריכוז כוח הרגש בצורה מסוימת, הוא מצית את האש. כשמשלבים, קצת כמו בכימיה, את עוצמת האוויר עם כוח האש שנוצר על ידי הרגש, תקבלו "אוויר של אש". כפי שאתם אולי יודעים, אוויר האש הזה מוזכר בפאוסט של גתה.[3] זה משהו שדורש השתתפות פנימית של האדם. לכן, רכיב אחד מופק ממרכיב קיים, אוויר, ואילו אנו בעצמנו מייצרים את השני, אש או חום. אוויר בתוספת אש נותנים את מה שאלכימאים כינו גופרית או אוויר אש בוהק. הנוכחות של אוויר האש הזה ביסוד מיימי היא העניין האסטרלי שעליו כתוב בתנ"ך, "ורוח אלוהים מרחפת על פני המים".[4]
היסוד השלישי מתעורר כאשר אנו מחלצים את כוח האדמה ולאחר מכן משלבים אותו עם כוחות הצליל הרוחני. התוצאה היא מה שנקרא כאן רוח האלוהים. זו הסיבה שזה נקרא גם רעם. רוחו האקטיבית של אלוהים היא רעם, אדמה ועוד צליל. לכן רוח האלוהים מרחפת מעל החומר האסטרלי.
המים המקראיים אינם מים רגילים, אלא מה שנקרא בעצם חומר אסטרלי. הם מורכבים מארבעה סוגי כוחות: מים, אוויר, אור ואש. מחרוזת ארבעת הכוחות הללו מתגלה לחזון האסטרלי כארבעת הממדים של המרחב האסטרלי. כלומר, זה מה שהם באמת. החלל האסטרלי נראה שונה מאוד מהעולם שלנו. הרבה תופעות אסטרליות לכאורה הן פשוט השלכות של היבטים מהעולם האסטרלי במרחב הפיזי.
כפי שאתם יכולים לראות, האסטרלי הוא חצי סובייקטיבי (כלומר הוא ניתן לסובייקט באופן פסיבי), חצי מים וחצי אוויר. מצד שני, אור ורגש (אש) הם אובייקטיביים, כלומר מופיעים על ידי פעילותו של הסובייקט. רק חלק מהאסטרלי ניתן למצוא בחוץ, כנתון לסובייקט בסביבתו. יש להוסיף את החלק השני על ידי פעילות משלכם. השאר מתקבל מכוחות המושגים והרגשות, ממה שניתן, באמצעות אובייקטיביזציה פעילה. בגלל זה, באסטרלי אנו מוצאים חומר סובייקטיבי-אובייקטיבי. בדוואכן יש רק אלמנט סובייקטיבי לחלוטין.
בגלל זה, בתחום האסטרלי אנו מוצאים יסוד שחייב להיווצר על ידי בני אדם. כל מה שאנחנו עושים כאן הוא רק סמל, ייצוג סמלי של העולמות העליונים, של העולם הדוואכני. העולמות האלה נכונים באופן שהצגתי לכם אותם בהרצאות האלה. את מה שיש בעולמות העליונים האלה אפשר להשיג רק באמצעות אפשרויות ראייה חדשות. האדם חייב לעשות משהו בעצמו כדי להגיע לעולמות האלה.
———————————————————————————-
- נראה ששטיינר התייחס לגרסה פשוטה יותר של אחת ממערכות הינטון. לא ברור מהקְשר ההרצאה אם שטיינר התכוון לצבעים כדי להציע תכונות ספציפיות של הממדים המתאימים, אך זה נראה לא סביר. תמלילים שונים של ההרצאה שונים באופן מהותי במקום זה, כנראה בשל דרכי ההתאמה השונות של השימוש בצבע (במיוחד לבן) של שטיינר, והעברתם מלוח לנייר לבן. ↑
- הממד הרביעי [1904], מאת הינטון, פרק י"ג, מכיל כמעט את אותו נימוק וצורות זהות. ↑
- פאוסט, מאת גתה, חלק א', סצנה 4, חדר הלימוד של פאוסט, פסוק 2065, היכן שמפיסטופלס מדבר. ↑
- בראשית פרק א: ראה התייחסות עמוקה של רודולף שטיינר לפסוק זה בסדרת ההרצאות: בראשית – סודות סיפור הבריאה המקראי (GA122), במיוחד ההרצאה של 20 באוגוסט 1910 – יצא לאור בעברית בהוצאת תלתן-חירות. ↑

